Глава I. Полимино и шахматные доски

В этой книге мы будем рассматривать полимино - фигуры, составленные из одноклеточных квадратов так, что каждый квадрат примыкает хотя бы к одному соседнему, имеющему с ним общую сторону. (Шахматист назвал бы это группировкой "по принципу ладьи", имея в виду, что поставленная на любую клетку полимино ладья, которая ходит на любое число клеток по вертикали или по горизонтали, но не по диагонали, сможет за конечное число ходов перейти на любую другую клетку того же полимино.)

Задачи с полимино очень характерны для комбинаторной геометрии - раздела математики, занимающегося вопросами взаимного расположения и комбинирования геометрических фигур. Это очень красивая, но еще почти не разработанная ветвь математики, поскольку общих методов в ней, по-видимому, очень мало, а известные ныне методы настолько примитивны, что не поддаются усовершенствованию. Многие встречающиеся в практике важные инженерные задачи - в первую очередь те, которые связаны в том или ином смысле с оптимальным расположением фигур заданной формы, - по существу относятся к комбинаторной геометрии. Цель настоящей главы двояка: во-первых, послужить введением в связанные с полимино математические головоломки и развлечения и, во-вторых, проиллюстрировать некоторые приемы и рассуждения, характерные для комбинаторной геометрии вообще.

Простейшие типы полимино - всевозможные комбинации из менее чем пять сгруппированных квадратов - изображены на рис. 1. В последующих комбинаторных задачах предполагается, что полимино можно вращать (то есть поворачивать на 90, 180 или 270°) и зеркально отражать (переворачивать), не меняя формы самих фигур (ср. с гл. VI, которая посвящена односторонним полимино, стр. 114).

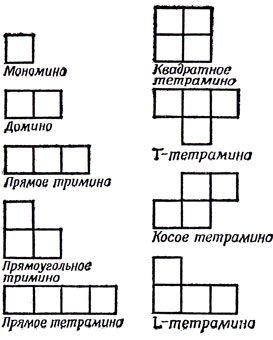
Рис. 1. Простейшие формы полимино