Функции класса L^2

В качестве приложения теории Лебега мы изложим обобщение теоремы Парсеваля (которую мы доказали лишь для непрерывных функций в гл. 8) и докажем теорему Рисса-Фишера для ортонормальных систем функций.

10.34. Определение. Пусть X - измеримое пространство. Мы будем говорить, что комплексная функция f принадлежит классу (μ) на X, если f измерима и

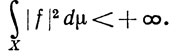
Если μ - мера Лебега, то мы будем писать просто f∈(μ). Если f∈(μ) (начиная с этого места мы будем опускать слова "на X"), то мы полагаем, по определению,

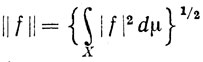
и называем число ||f|| нормой функции f.

10.35. Теорема. Пусть f∈(μ) и g∈(μ). Тогда fg∈(μ) и

(97)

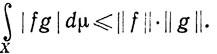
Это неравенство, как и в случае рядов и интегралов Римана, называется неравенством Шварца. Как и в рассмотренных ранее случаях, оно вытекает из неравенства

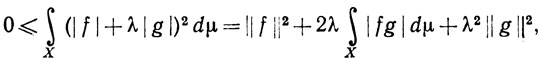
которое выполняется при всяком вещественном λ.

10.36. Теорема. Если f∈(μ) и g∈(μ), то f+g ∈(μ) и

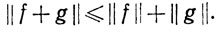
Доказательство. Неравенство Шварца показывает, что

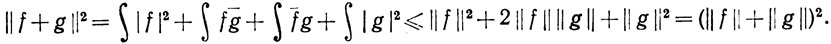
10.37. Замечание. Определим расстояние между двумя функциями f и g в (μ), полагая его равным ||f-g||. Ясно, что все, кроме одного условия п. 2.17, выполняются. Дело в том, что из равенства ||f-g|| = 0 не следует, что f(x) = g(x) при всех х, а следует только, что f(x) = g(x) при почти всех х. Таким образом, если мы отождествим функции, отличающиеся только на множестве меры нуль, то (μ) оказывается метрическим пространством.

Рассмотрим теперь на сегменте вещественной оси с мерой Лебега.

10.38. Теорема. Непрерывные функции образуют всюду плотное множество в на [a, b].

Точнее, это значит, что для любой функции f∈ на [а, b] и любого ε>0 существует функция g, непрерывная на [а, b] и такая, что

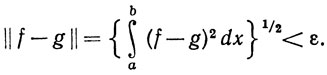
Доказательство. Мы будем говорить, что последовательность {g_n} аппроксимирует функцию f в , если ||f-g_n||→0 при n→∞.

Пусть A - замкнутое подмножество сегмента [а, b], а К_А - характеристическая функция этого подмножества. Положим

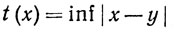
(y∈A)

и

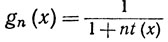
(n = 1, 2, 3, ...).

Тогда функция g_n непрерывна на [a, b], g_n(x) = 1 на А и g_n(x)→0 на В, где В = [а, b] - А. Значит,

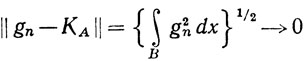
по теореме 10.32. Итак, характеристическую функцию замкнутого множества можно аппроксимировать в последовательностью непрерывных функций.

Согласно (39), то же верно и в отношении характеристической функции любого измеримого множества, и, стало быть, в отношении любой простой измеримой функции.

Если f≥0 и f∈, то пусть {s_n} - такая монотонно возрастающая последовательность простых неотрицательных измеримых функций, что s_n(х)→f(x) при всех х. Теорема 10.32 показывает, что ||f-s_n||→0, так как |f-s_n|²≤|f|².

Отсюда следует утверждение теоремы и в общем случае.

10.39. Определение. Мы будем говорить, что последовательность комплексных функций {φ_n} есть ортонормальная система функций на измеримом пространстве X, если

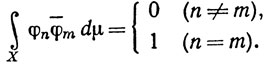
В частности, должно выполняться включение φ_n∈(μ). Если f∈(μ) и если

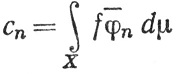
то мы будем писать

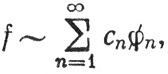
как в определении 8.10.

Аналогично распространяется на (или даже на 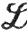) определение тригонометрического ряда Фурье на [-π, π]. Теоремы 8.11 и 8.12 (неравенство Бесселя) верны для любой f∈(μ). Доказательства дословно те же.

Теперь мы можем доказать теорему Парсеваля.

10.40. Теорема. Пусть

(98)

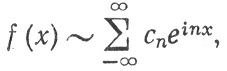
где f∈ на [-π, π]. Пусть s_n есть n-я частная сумма ряда (98). Тогда

(99)

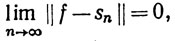
(100)

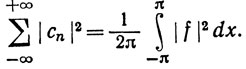
Доказательство. Пусть ε>0. По теореме 10.38 существует непрерывная функция g, такая, что

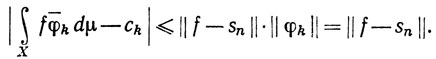
Легко видеть, что функцию g можно подобрать так, чтобы удовлетворялось условие g(π) = g(-π). Тогда g можно продолжить на всю прямую как непрерывную периодическую функцию. По теореме 8.16 существует тригонометрический многочлен Т степени N, такой, что

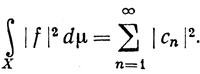
Значит, по теореме 8.11 (в случае ) при n≥N имеем

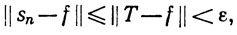
откуда и следует (99). Равенство (100) можно вывести из (99) так же, как при доказательстве теоремы 8.16

Следствие. Если f∈ на [-π, π] и если

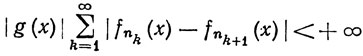
то ||f|| = 0.

Таким образом, если две функции имеют одинаковые ряды Фурье, то они совпадают почти всюду.

10.41. Определение. Пусть f и f_n∈(μ) (n = 1, 2, 3, ...) Будем говорить, что последовательность {f_n} сходится к f в (μ), если ||f_n-f||→0. Будем говорить, что {f_n} - последовательность Коши в (μ), если для любого ε>0 существует целое N, такое, что из n≥N, m≥N следует неравенство ||f_n-f_m||≤ε.

10.42. Теорема. Если {f_n} - последовательность Коши в (μ), то существует функция f∈(μ), такая, что {f_n} сходится к f в (μ).

Другими словами, (μ) - полное метрическое пространство.

Доказательство. Поскольку {f_n} - последовательность Коши, то мы можем найти такую строго возрастающую последовательность {n_k}, k = 1, 2, 3, ..., что

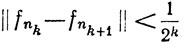
Выберем функцию g∈(μ). В силу неравенства Шварца,

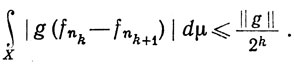
Значит,

(101)

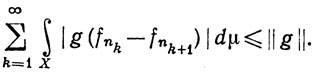
По теореме 10.30 мы можем поменять местами суммирование и интегрирование в (101). Следовательно,

(102)

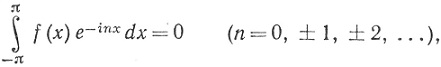
почти всюду на X. Поэтому

(103)

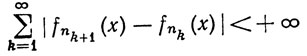
почти всюду на X. Действительно, если бы ряд (103) расходился на множестве Е положительной меры, то мы могли бы выбрать функцию g отличной от нуля на множестве положительной меры, содержащемся в Е, и прийти к противоречию с (102). Поскольку k-я частная сумма ряда

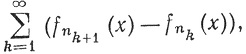
сходящегося почти всюду на X, совпадает с

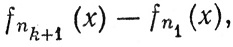
то равенство

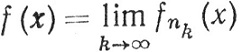
определяет f(x) для почти всех х∈Х, и неважно, как мы определим f(х) в остальных точках множества X.

Теперь мы покажем, что функция f обладает нужными свойствами. Пусть ε>0. Возьмем число N, указанное в определении 10.41. Если n_k>N, то теорема Фату показывает, что

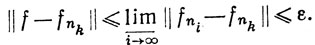
Таким образом, f-f_nk∈(μ), а так как f = (f-f_nk) + f_nk, то f∈(μ). Кроме того, ввиду произвольности числа ε>0

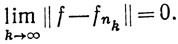
Наконец, из неравенства

(104)

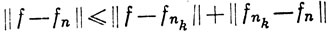
следует, что последовательность {f_n} сходится к функции f в (μ); действительно, выбирая n и n_k достаточно большими, мы можем сделать оба слагаемых в правой части неравенства (104) сколь угодно малыми.

10.43. Теорема Рисса-Фишера. Пусть {φ_n} - ортонормальная система на X. Допустим, что ряд 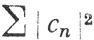сходится, и положим s_n = c₁φ₁+...+c_nφ_n. Тогда существует функция f∈(μ), такая, что {s_n} сходится к f в (μ), причем

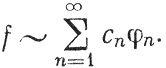
Доказательство. Если n>m, то

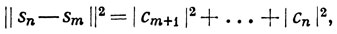
так что {s_n} - последовательность Коши в (μ). По теореме 10.42 существует функция f∈(μ), такая, что

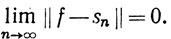
Теперь при n>k

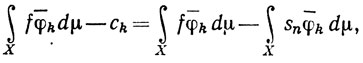
так что

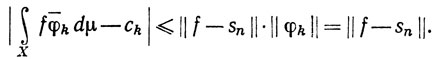
Полагая n→∞, получаем

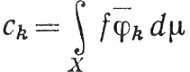
(k = 1, 2, 3, ...),

и доказательство закончено.

10.44. Определение. Ортонормальная система {φ_n} называется полной, если из того, что f∈(μ) и

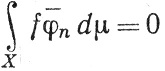
следует, что ||f|| = 0.

Из теоремы 10.40 и равенства Парсеваля (100) следует полнота тригонометрической системы. Обратно, равенство Парсеваля выполняется для любой полной ортонормальной системы.

10.45. Теорема. Пусть {φ_n} - полная ортонормальная система. Если f∈(μ) и если

(105)

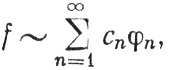
то

(106)

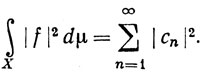
Доказательство. Из неравенства Бесселя следует, что ряд 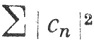сходится. Положим

В силу теоремы Рисса-Фишера существует функция g∈(μ), такая, что

(107)

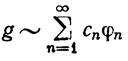
и 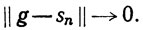Значит, 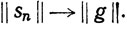Поскольку

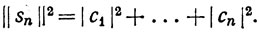
(108)

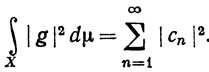
Теперь из (105), (107) и полноты системы {φ_n} следует, что ||f-g|| = 0, так что из (108) следует (106).

Комбинируя теоремы 10.43 и 10.45, мы приходим к очень интересному выводу: каждая полная ортонормальная система порождает взаимно однозначное соответствие между функциями f∈(μ) (причем функции, совпадающие почти всюду, отождествляются) и последовательностями {c_n} для которых сходится ряд 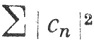Представление

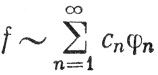
и равенство Парсеваля показывают, что (μ) можно рассматривать как бесконечномерное евклидово пространство (так называемое "гильбертово пространство"), в котором точка f имеет координаты с_n, а функции φ_n служат координатными векторами.