Упражнения

1. Пусть f≥0 и 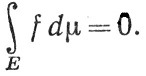Доказать, что f(x) = 0 почти всюду на Е.

Указание. Пусть Е_n - подмножество множества Е, на котором f(x)>¹/_n. Положим A = ∪E_n; р(А) = 0 тогда и только тогда, когда μ(E_n) = 0 при всех n.

2. Если 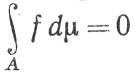для всякого измеримого подмножества А множества Е, то f(x) = 0 почти всюду на Е.

3. Пусть {f_n} - последовательность измеримых функций. Доказать, что множество точек х, в которых {f_n(х)} сходится, измеримо.

4. Если f∈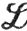(μ) на Е, а функция g ограничена и измерима на E, то fg∈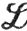(μ) на Е.

5. Положим

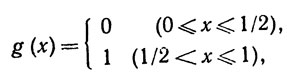
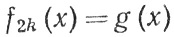
(0≤x≤1),

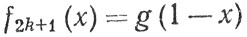
(0≤x≤1).

Тогда 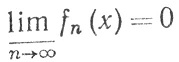(0≤x≤1), но

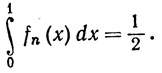
(ср. с (77)).

6. Пусть

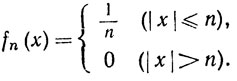
Тогда f_n(x)→0 равномерно на R¹, но

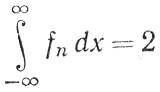
(n = 1, 2, 3, ...).

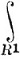(Мы пишем вместо .) Таким образом, из равномерной сходимости не следует ограниченная сходимость в смысле теоремы 10.32. Однако на множествах конечной меры равномерно Сходящиеся последовательности ограниченных функций сходятся ограниченно.

7. Найти условие, необходимое и достаточное для того, чтобы f∈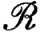(α) на [а, b].

Указание. Рассмотреть пример 10.6 (b) и теорему 10.33.

8. Если f∈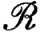 на [а, b] и если 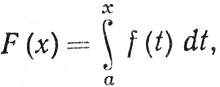то F' (х) = f(х) почти всюду на [а, b].

9. Доказать, что функция F, заданная равенством (95), непрерывна на [а, b].

10. Если μ(Х)<+∞ и f∈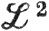(μ) на X, то f∈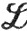(μ) на A.

Если

то это, вообще говоря, неверно. Например, если

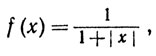
то f∈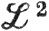 на R¹, но f∉ 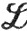на R¹.

11. Если f,g∈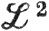(μ) на X, то определим расстояние между f и g, полагая его равным

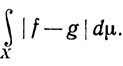
Доказать, что 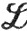(μ) - полное метрическое пространство.

12. Допустим, что

(a) |f(x, y)|≤1, если 0≤x≤1, 0≤y≤1,

(b) при фиксированном х функция f(x, у) непрерывна по у,

(c) при фиксированном у функция f(х, у) непрерывна по х.

Положим

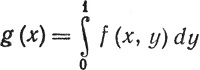
(0≤x≤1).

Непрерывна ли функция g?

13. Рассмотрим функции

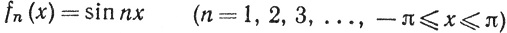
как точки пространства 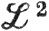. Доказать, что множество этих точек замкнуто и ограничено, но не компактно.

14. Доказать, что комплексная функция f измерима тогда и только тогда, когда множество f^-1(V) измеримо, каково бы ни было открытое плоское множество V.

15. Пусть М - кольцо элементарных подмножеств промежутка (0, 1]. Если 0<а≤b≤1, то положим

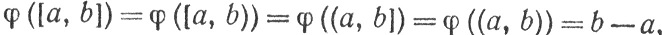
и

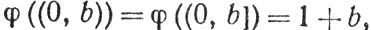
если 0<b≤1. Показать, что этим определена аддитивная функция множества на М, которая не регулярна и не может быть продолжена до функции, счетно-аддитивной на σ-кольце.

16. Пусть {n_k} - возрастающая последовательность положительных целых чисел, а Е - множество всех точек x∈(-π, π), в которых сходится последовательность {sin n_kx}. Доказать, что m(E) = 0.

Указание. При любом A⊂E

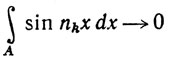
и

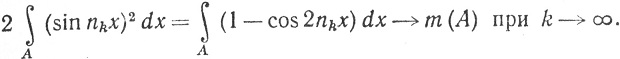
17. Допустим, что Е⊂(-π, π), m(E)>0, δ>0. Воспользоваться неравенством Бесселя для доказательства того, что имеется не более чем конечное число таких целых n, что sin nx>δ при всех х∈Е.

18. Пусть f∈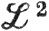(μ), g∈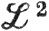(μ). Доказать, что

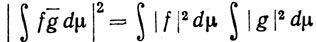
тогда и только тогда, когда существует такое число с, что g(x) = cf(x) почти всюду. (Ср. с теоремой 10.35.)