Интегрирование комплексных функций

Пусть f - комплекснозначная функция, определенная на пространстве с мерой X, f = u+iv, где u и v - вещественны. Мы будем говорить, что функция f измерима, если обе функции u и v измеримы.

Легко проверить, что суммы и произведения комплексных измеримых функций снова измеримы. Из теоремы 10.18 следует, что |f| - измеримая функция, если измерима комплексная функция f, так как

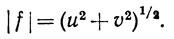
Допустим, что μ - мера на X, Е - измеримое подмножество X, а f - комплексная функция, определенная на X. Мы будем говорить, что f∈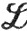(μ) на Е, если f измерима и

(96)

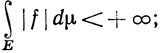
при этом мы полагаем, по определению,

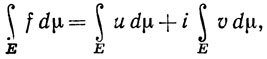
если выполнено (96). Ясно, что (96) выполняется тогда и только тогда, когда u∈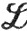(μ) и v∈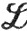(μ) на Е, так как |u|≤|f|, |v|≤|f|, |f|≤|u|+|v|.

Теоремы 10.23 (a), (d), (e), (f), 10.24 (b), 10.26, 10.27, 10.29, 10.32 могут быть перенесены на интегралы Лебега от комплексных функций. Доказательства совсем просты, и только доказательство теоремы 10.26 представляет некоторый интерес. Вот оно.

Если f∈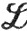(μ) на Е, то существует комплексное число с, |с| = 1, такое, что

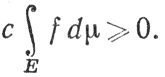
Положим g = cf = u + iv, где u и v вещественны. Тогда

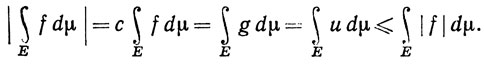
Заметим, что число ∫ g dμ вещественно (это следует из первых двух равенств).