Сравнение с интегралом Римана

Наша следующая теорема показывает, что каждая функция, интегрируемая по Риману на некотором сегменте, интегрируема на этом сегменте и по Лебегу, и что функции, интегрируемые по Риману, подчиняются довольно ограничительным условиям непрерывности. Теория Лебега позволяет интегрировать функции гораздо более широкого класса. Однако самое значительное ее преимущество состоит, вероятно, в той свободе, с которой в интегралах Лебега оказывается возможным производить операции предельного перехода; с этой точки зрения теоремы о сходимости составляют суть лебеговской теории.

Одна из трудностей, встречающихся в теории Римана, заключается в том, что предел последовательности функций, интегрируемых по Риману (или даже непрерывных), может уже не быть интегрируемым по Риману. В теории Лебега эта трудность почти исключается, так как предел последовательности измеримых функций снова измеримая функция.

Пусть пространством X с мерой служит сегмент [а, b] вещественной прямой с μ = m (мера Лебега), а - множество всех подмножеств сегмента X, измеримых по Лебегу. Вместо

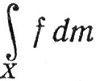
для интеграла Лебега функции f по сегменту [а, b] принято употреблять привычное обозначение

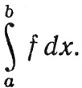
Чтобы отличить лебегов интеграл от интеграла Римана, мы будем этот последний обозначать так:

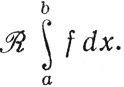
10.33. Теорема. (а) Если f∈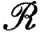 на [а, b], то f∈ 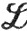на [а, b] и

(87)

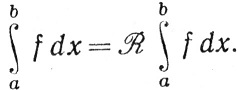
(b) Пусть функция f ограничена на [а, b]. Тогда f∈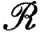 на [а, b] тогда и только тогда, когда функция f непрерывна почти всюду на [а, b].

Доказательство. Пусть функция f ограничена. Пусть {P_k} - такая последовательность разбиений сегмента [а, b], что P_k+1 - измельчение разбиения Р_k и μ(Р_k)→0 при k→∞ (в этом доказательстве μ обозначает не меру, а диаметр разбиения). Если Р_k - разбиение

то положим U_k(a) = L_k(a) = f(а) и

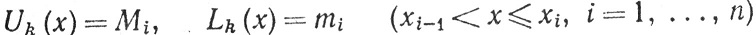
(обозначения те же, что и в п. 6.1). Тогда

(88)

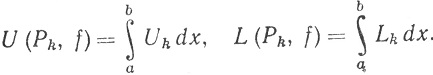
Поскольку P_k+1 - измельчение разбиения P_k, то

(89)

Положим

(90)

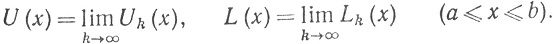
Теперь допустим, что f∈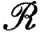. Ввиду того что μ(P_k)→0,

(91)

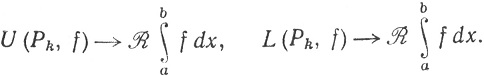
Это последнее соотношение не было явно сформулировано в гл. 6 в виде теоремы, но его, конечно, легко вывести из доказательства теоремы 6.14 [см. формулы (28) и (29)]. Согласно (89) и (90),

(92)

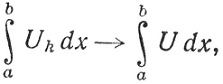
так что из (88), (91) и (92) следует, что

(93)

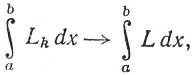
Поскольку L(x)≤f(x)≤U(x) на [a, b], то первое из равенств (93) показывает, что

(94)

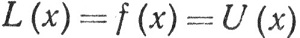
почти всюду на [а, b] (упражнение 1). Поскольку L и U измеримы, то это верно и в отношении f. Значит, f∈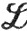, и (87) следует из (93) и (94).

Теперь допустим, что х не принадлежит никакому из разбиений P_k (отметим, что множество всех точек, входящих в состав, какого-нибудь разбиения P_k, счетно и потому имеет меру нуль) Совсем легко показать, что тогда функция f непрерывна в точке х в том и только в том случае, когда U (x) = L(x).

Таким образом, если f∈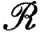 на [а, b], то, как показывает (94), функция f непрерывна почти всюду на [а, b]. Обратно, если f непрерывна почти всюду на [а, b], то (94) выполнено. Значит, выполнено первое из равенств (93), и, как показывают (92) и (88), для всякого ε>0 можно найти такое k, что

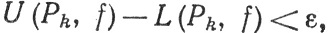
следовательно, по теореме 6.6, f∈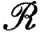 на [а, b].

Многие соотношения между интегрированием и дифференцированием функций переносятся и в лебеговскую теорию. Если f∈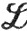 на [а, b] и

(95)

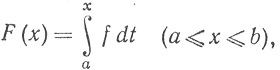
то F'(х) = f(х) почти всюду на [а, b].

Обратно, если функция F дифференцируема в каждой точке сегмента [а, b] ("почти всюду" здесь недостаточно!) и если F'∈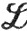 на [а, b], то

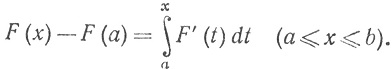
Доказательства можно найти в любой из достаточно подробных книг по теории интеграла.