Интегрирование

Мы определим интегрирование на измеримом пространстве X с σ-кольцом 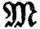измеримых множеств и с мерой μ. Читатель, желающий иметь перед глазами более конкретную ситуацию, может представлять себе X как прямоугольник или как вещественную прямую, a μ - как меру Лебега.

10.21.Определение. Допустим, что функция

(51)

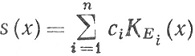
(х∈Х,c_i>0)

измерима, и пусть Е∈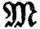. Положим

(52)

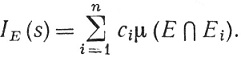
Если функция f измерима и неотрицательна, то мы определим

(53)

где верхняя грань берется по всем простым функциям, таким, что 0≤s≤f.

Левая часть равенства (53) называется интегралом Лебега функции f относительно меры μ no множеству Е. Заметим, что интеграл может быть равным +∞.

Легко проверить, что

(54)

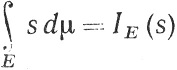
для любой неотрицательной простой измеримой функции s.

10.22. Определение. Пусть функция f измерима. Рассмотрим два интеграла

(55)

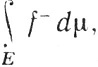
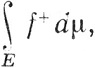
где f⁺ и f^- определены, как в (47).

Если хотя бы один из интегралов (55) конечен, то мы полагаем, по определению,

(56)

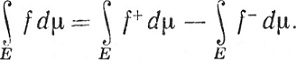
Если оба интеграла (55) конечны, то и разность (56) конечна, и мы говорим, что функция f интегрируема (или суммируема) на множестве Е в смысле Лебега по отношению к мере μ; мы пишем f∈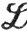(μ) на множестве Е. Если μ = m, то обычное обозначение таково: f∈ 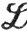на множестве Е.

Эта терминология может вызвать небольшую путаницу: если (56) равно +∞ или -∞, то интеграл функции f по множеству Е определен, хотя функция f и не интегрируема в только что разъясненном смысле слова; f интегрируема по множеству Е только тогда, когда ее интеграл по этому множеству конечен.

10.23. Замечания. Следующие свойства очевидны:

(а) Если f измерима и ограничена на множестве Е и μ(E)<+∞, то f∈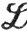(μ) на Е.

(b) Если f измерима, причем а≤f(x)≤b при х∈Е, а μ(E)<+∞, то

(c) Если f и g∈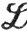(μ) на Е и если f(x)̤g(x) при всех x∈E, то

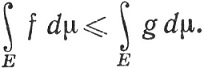
(d) Если f∈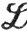(μ) на E, то cf∈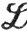(μ) на Е, каково бы ни было конечное число с, и

(e) Если μ(E) = 0, а f - измерима, то

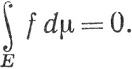
(f) Если f∈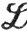(μ) на E, А∈ 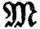и А⊂Е, то f∈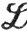(μ) на A.

10.24. Теорема. (а) Пусть f измерима и неотрицательна на множестве X. Для А∈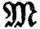 положим

(57)

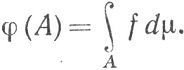
Тогда функция φ счетно-аддитивна на .

(b) То же верно, если f∈(μ) на X.

Доказательство. Ясно, что (b) следует из (а), если мы запишем f = f⁺ - f^- и применим (а) к f⁺ и f^-.

Чтобы доказать (а), мы должны показать, что

(58)

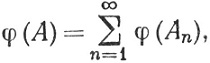
если А_n∈ (n = 1, 2, 3, ...), A_i∩A_j = 0 при i≠j и

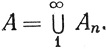
Если f - характеристическая функция, то счетная аддитивность функции φ - то же самое, что счетная аддитивность функции μ, так как

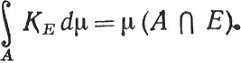
Если f - простая функция, то f имеет вид (51) и утверждение теоремы также выполняется.

В общем случае для каждой простой измеримой функции s, такой, что 0≤s≤f, имеем

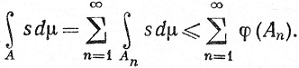
Поэтому, согласно (53),

(59)

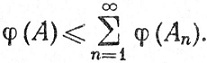
Заметим теперь, что если φ(A_n) = +∞ при каком-нибудь n, то (58) тривиально, так как φ(A)≥φ(A_n). Поэтому пусть φ(А_n)<+∞ при всех n.

Для заданного ε>0 выберем измеримую функцию s так, что 0≤s≤f и

(60)

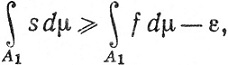
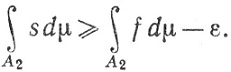
Ясно, что

так что

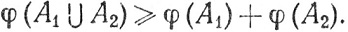
Следовательно, при каждом n

(61)

Поскольку A⊃A₁⊂...⊂A_n, то из (61) следует, что

(62)

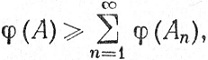
и (58) вытекает из (59) и (62).

Следствие. Если А∈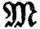, В⊂A, μ(A - B) = 0 и функция f измерима, то

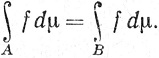
Поскольку A = B&38834;(A - B), это следует из замечания 10.23(e).

10.25. Замечание. Приведенное выше следствие показывает, o что множествами меры нуль при интегрировании можно пренебречь.

Если множество

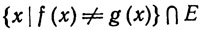
имеет меру нуль, то мы будем писать f~g на Е. Тогда f~f; из f~g следует, что g~f, и из f~g, g~h следует, что f~h. Это значит, что отношение ~ есть отношение эквива-

Если f~g на E, то мы, очевидно, имеем для любого измеримого подмножества A множества Е

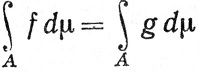
при условии, что эти интегралы существуют^*.

^* (Более того, если существует один из этих интегралов, то существует и другой.- Прим. перев.)

Если свойство Р выполняется для каждого х∈ Е-А и если μ(A) = 0, то обычно говорят, что Р выполняется для почти всех х∈Е или что Р выполняется почти всюду на Е. (Смысл этого "почти всюду" зависит, разумеется, от той конкретной меры, которую мы рассматриваем. В литературе, если не оговорено противное, обычно имеют в виду меру Лебега.)

Если f∈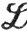(μ) на Е, то ясно, что значение f(х) конечно почти всюду на Е. Поэтому в большинстве случаев мы можем, не умаляя общности, с самого начала предполагать, что функции, с которыми мы имеем дело, принимают только конечные значения.

10.26. Теорема. Если f∈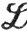(μ) на Е, то и |f|∈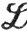(μ) на Е и

(63)

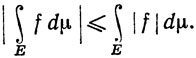
Доказательство. Запишем Е = А∪В, где f(х)≥0 на A и f(x)<0 на В. По теореме 10.24

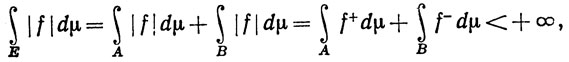
так что |f|∈(μ). Поскольку f≤|f| и -f≤|f|, мы видим, что

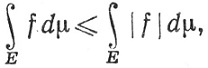
откуда и следует (63).

Поскольку из интегрируемости функции f следует интегрируемость функции |f|, то интеграл Лебега часто называют абсолютно сходящимся. Конечно, можно определить и неабсолютно сходящиеся интегралы, и при изучении некоторых проблем это даже существенно. Но у этих интегралов отсутствуют наиболее полезные свойства интеграла Лебега, и они играют в анализе несколько менее важную роль.

10.27. Теорема. Пусть функция f измерима на Е, |f|≤g и g∈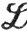(μ) на Е. Тогда f∈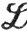(μ) на Е.

Доказательство. Имеем f⁺≤g и f^-≤g.

10.28. Теорема Лебега о монотонной сходимости^*. Пусть Е∈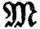. Пусть {f_n} - такая последовательность измеримых функций, что

(64)

Пусть функция f определена равенством

(65)

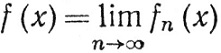
Тогда

(66)

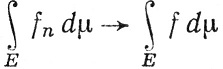
^* (Эта теорема обычно называется теоремой Б. Леви.- Прим. перев.)

Доказательство. Согласно (64), существует такое α, что

(67)

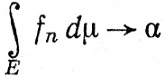
при n→∞, а так как ∫ f_n ≤∫f, то

(68)

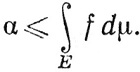
Выберем с так, чтобы 0<с<1, и пусть s - простая измеримая функция, такая, что 0≤s≤f. Положим

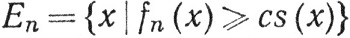
( n =1, 2, 3,...).

Согласно (64), Е₁⊂Е₂⊂Е₃⊂ ..., а в силу (65)

(69)

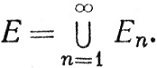
При любом n

(70)

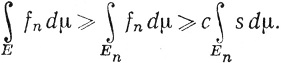
Устремим в (70) n к ∞. Поскольку интеграл - счетно-аддитивная функция множества (теорема 10.24), то, как показывает (69), можно применить теорему 10.3 к последнему интегралу в (70), и мы получим

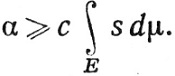
Устремляя с к единице, мы видим, что

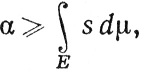
а из (53) следует, что

(72)

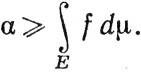
Теорема следует теперь из (67), (68) и (72).

10.29. Теорема. Пусть f = f₁ + f₂, где f_i∈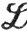(μ) на Е (i = 1, 2). Тогда f∈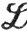(μ) на Е и

(73)

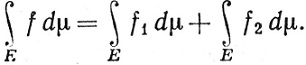
Доказательство. Сначала допустим, что f₁≥0, f₂≥0. Если f₁ и f₂ - простые функции, то (73) тривиально следует из (52) и (54). В общем случае выберем монотонно возрастающие последовательности {s'_n}, {s"_n} неотрицательных измеримых простых функций, сходящихся к f₁ и f₂. Теорема 10.20 показывает, что это возможно. Положим s_n = s'_n+s"_n.

Тогда

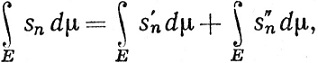
и (73) получится, если мы устремим n к ∞ и применим теорему 10.28.

Теперь допустим, что f₁≥0, f₂≤0. Положим

Тогда функции f, f₁ и -f₂ неотрицательны на A. Значит,

(74)

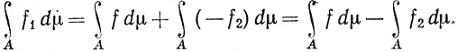
Аналогично функции -f, f₁ и -f₂ неотрицательны на В, так что

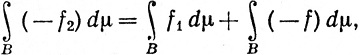
или

(75)

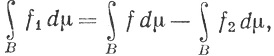
и (73) вытекает из (74) и (75).

В общем случае множество E можно разложить на четыре множества E_i, на каждом из которых f₁(x) и f₂(х) сохраняют знак. Из доказанного следует, что

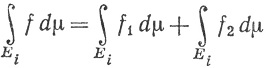
(i = 1, 2, 3, 4),

и (73) получается, если мы просуммируем эти равенства.

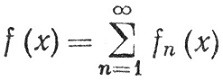
Теорему 10.28 можно следующим образом переформулировать в терминах рядов функций.

10.30. Теорема. Пусть Е∈. Если {f_n} - последовательность неотрицательных измеримых функций и

(76)

(x∈E),

то

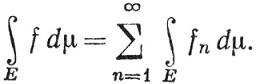
Доказательство. Частные суммы ряда (76) образуют монотонно возрастающую последовательность.

10.31. Теорема Фату. Пусть E∈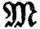. Если {f_n} - последовательность неотрицательных измеримых функций и

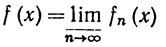
то

(77)

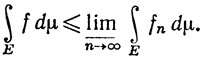
В (77) может иметь место строгое неравенство. Пример указан в упражнении 5.

Доказательство. Положим

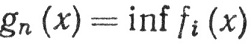
(i≥n)

при n = 1, 2, 3, ... и х∈Е.

Тогда функция g_n измерима на множестве Е и

(78)

(79)

(80)

Согласно (78), (80) и теореме 10.28,

(81)

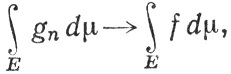
так что (77) следует из (79) и (81).

10.32. Теорема Лебега об ограниченной сходимости. Пусть Е∈. Пусть {f_n} - такая последовательность измеримых функций, что

(82)

при n→∞. Если существует функция g, такая, что

(83)

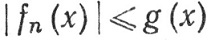
(n = 1, 2, 3, ..., x∈E),

и g∈(μ) на Е, то

(84)

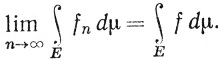
Неравенство (83) означает, что функция g ограничивает последовательность {f_n}; этим объясняется название теоремы. В силу п. 10.25, утверждение теоремы остается верным, если (82) выполняется почти всюду на Е.

Доказательство. Заметим сначала, что из теоремы 10.27 следует, что f_n∈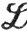(μ) и f∈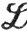(μ) на E.

Теорема Фату показывает, что

так как f_n + g≥0; иначе говоря,

(85)

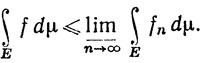
Аналогично, поскольку g-f_n≥0, то

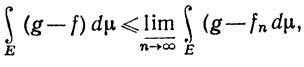
так что

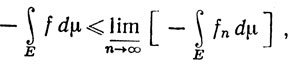
а это значит, что

(86)

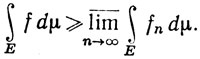
Существование предела в (84) и равенство (84) теперь следуют из (85) и (86).

Следствие. Если μ(E)∈+∞, последовательность {f_n} равномерно ограничена на Е и f_n(х)→f(x) при всех х∈Е, то выполняется (84).