Простые функции

10.19. Определение. Пусть s - вещественная функция, определенная на множестве X. Если множество значений функции s конечно, то мы будем говорить, что s - простая функция.

Пусть Е⊂X, и пусть

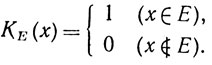
К_Е называется характеристической функцией множества Е.

Пусть множество значений функции s состоит из различных чисел с₁, ..., с_n. Пусть

Тогда

(49)

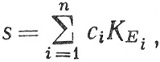
т. е. каждая простая функция представляет собой конечную линейную комбинацию характеристических функций. Ясно, что s измерима тогда и только тогда, когда множества Е₁, ..., Е_n измеримы.

Оказывается, любую функцию можно приблизить простыми функциями,

10.20. Теорема. Пусть f - вещественная функция, определенная на множестве X. Тогда существует последовательность {s_n} простых функций, такая, что s_n (х)→f(x) при n&38594;∞ для всякого х∈Х. Если функция f измерима, то можно выбрать последовательность {s_n} так, чтобы все функции sn тоже были измеримы. Если f≥0, то последовательность {s_n} можно считать монотонно возрастающей.

Доказательство. Если f&38805;0, то положим

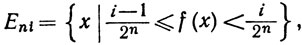
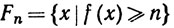
при n = 1, 2, 3, ..., i = 1, 2, ... n2ⁿ, Пусть

(50)

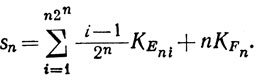
В общем случае запишем f = f ⁺ - f ^- и применим предыдущую конструкцию к f ⁺ и f ^-.

Заметим, что последовательность {s_n}, заданная равенством (50), сходится к f равномерно, если f ограничена.