Измеримые функции

10.13. Определение. Пусть f - функция, определенная на измеримом пространстве X со значениями в расширенной системе вещественных чисел. Функция f называется измеримой, если множество

(42)

измеримо при каждом вещественном а.

10.14. Пример. Если X = R^p, а = (μ) - в соответствии с определением 10.9,- то каждая непрерывная функция f измерима, так как в этом случае множество (42) открыто.

10.15. Теорема. Следующие условия эквивалентны:

(43)

(44)

(45)

(46)

Доказательство. Отношения

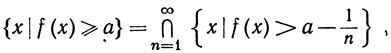
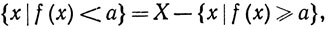
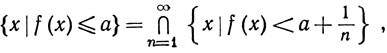
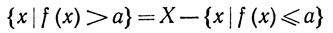
последовательно показывают, что из (43) следует (44), из (44) следует (45), из (45) следует (46), а из (46) следует (43).

Значит, каждое из этих условий можно использовать вместо (42) для определения измеримости.

10.16. Теорема. Если f измерима, то измерима и |f|.

Доказательство:

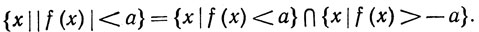
10.17. Теорема. Пусть {f_n} - последовательность измеримых функций. При х∈Х положим

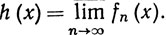
Тогда функции g и h измеримы.

Конечно, то же верно и в отношении нижней грани и нижнего предела.

Доказательство.

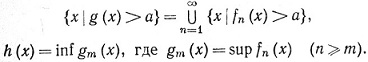
Следствия. (а) Если f и g измеримы, то max (f, g) и min (f, g) измеримы. Если

(47)

то, в частности, f⁺ и f^- измеримы.

(b) Предел сходящейся последовательности измеримых функций-измеримая функция.

10.18. Теорема. Пусть f и g - измеримые конечные вещественные функции, определенные на множестве X, пусть функция F вещественна и непрерывна на R², и пусть

Тогда функция h измерима.

В частности, функции f + g и fg измеримы.

Доказательство. Пусть G_α = {(u, v)|F(u, v)>a}. Тогда G_α - открытое подмножество пространства R² и

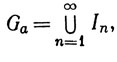
где {I_n} - последовательность открытых прямоугольников:

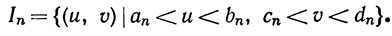
Поскольку множество

измеримо, то множество

измеримо. Значит, то же верно и в отношении множества

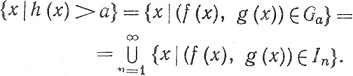
Подводя итоги, мы можем сказать, что все обычные операции анализа, включая операции, связанные с предельным переходом, будучи примененными к измеримым функциям, приводят снова к измеримым функциям; иными словами, все функции, с которыми обычно встречаются, измеримы.

То, что эта формулировка тем не менее довольно груба, видно, однако, из следующего замечания: если h(x) - f(g(x)), где функция f измерима, a g непрерывна, то функция h не обязательно измерима.

Читатель, возможно, заметил, что в нашем обсуждении измеримых функций нигде не упоминалась мера. В самом деле, класс функций, измеримых на X, зависит только от σ-кольца (обозначения те же, что в п. 10.12). Например, можно говорить о функциях, измеримых по Борелю на R^p, т. е. о функциях f, для которых множество

всегда борелевское, не упоминая при этом никакой конкретной меры.