Построение меры Лебега

10.4. Определение. Пусть R^p обозначает р-мерное евклидово пространство. Прямоугольником в R^p мы называем множество всех точек x = (x₁, ..., х_р), таких, что

(10)

или же множество точек, определяемое неравенствами (10), в которых некоторые (или все) знаки ≤ заменены на <;. Возможность равенства a_i = b_i при каком-нибудь значении i не исключается; в частности, пустое множество - тоже прямоугольник^*.

^* (Однако возможность неравенства а_i&362;b_i - следует исключить заранее, так как в противном случае число m(∅) (см. ниже) не будет определено однозначно.- Прим. перев.)

Если A - объединение конечного числа прямоугольников, то говорят, что A - элементарное множество.

Пусть I - прямоугольник; положим, по определению,

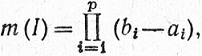
вне зависимости от того, включается или нет знак равенства в неравенства (10).

Если А = I₁∪...∪I_n и эти прямоугольники попарно не пересекаются, то мы полагаем

(11)

Обозначим буквой множество всех элементарных подмножеств пространства R^p.

Теперь следует убедиться в том, что

(12)

- кольцо, но не σ-кольцо.

(13)

Если А∈, то A представимо в виде объединения непересекающихся прямоугольников.

(14)

Если A∈, то m(А) действительно определено равенством (11). Это значит, что, исходя из двух различных представлений множества А в виде объединения непересекающихся прямоугольников, мы получим одно и то же значение m(А).

(15)

Функция m аддитивна на .

Заметим, что если р = 1, 2, 3, то m - это соответственно длина, площадь и объем.

10.5. Определение. Неотрицательная аддитивная функция множества φ, определенная на , называется регулярной, если верно следующее: для любого А∈ и любого числа ε>0 существуют множества F∈, G∈, такие, что F замкнуто, G открыто, F⊂A⊂G и

(16)

10.6.Примеры.(а) Функция множества m регулярна. Если А - прямоугольник, то требование определения 10.5 выполняется тривиальным образом. Общий случай следует из (13).

(b) Положим R^р = R¹, и пусть α - монотонно возрастающая функция, определенная на R¹. Положим

Здесь [а, b) - множество всех чисел х, таких, что a≤x<b, и т. д. Эти множества следует различать из-за возможных разрывов функции α. Если μ определить на элементарных множествах, как в (11), то функция μ оказывается регулярной на . Доказательство точно такое же, как в (а).

Наша следующая цель состоит в доказательстве того, что каждая функция множества, регулярная на , может быть продолжена до счетно-аддитивной функции множества, определенной на σ-кольце, содержащем .

10.7.Определение. Пусть функция μ аддитивна, регулярна, неотрицательна и конечна на . Рассмотрим счетные покрытия какого-нибудь множества Е⊂R^p открытыми элементарными множествами А_n:

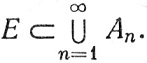
Положим, по определению,

(17)

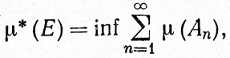
где нижняя грань берется по всем счетным покрытиям множества Е открытыми элементарными множествами. Число μ^* (Е) называется внешней мерой множества Е, соответствующей функции μ.

Ясно, что μ^*(Е)≥0 при всех Е и что

(18)

если Е₁⊂Е₂.

10.8.Теорема. (а) Для любого А∈ имеем μ^*(A) = μ(A).

(b) Если 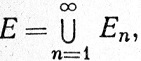то

(19)

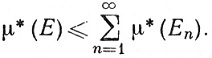
Отметим, что (а) означает, что функция μ^* - продолжение функции μ с кольца на множество всех подмножеств пространства R^p. Свойство (19) называется полуаддитивностью.

Доказательство. Пусть А∈ и ε>0.

Из регулярности меры μ следует, что множество А содержится в некотором открытом элементарном множестве G, таком, что μ(G)≤μ(A) + ε. Поскольку μ^*(A)≤μ(G) и поскольку число ε произвольно, то

(20)

По определению μ^* существует такая последовательность {А_n} открытых элементарных множеств, объединение которых содержит множество A, что

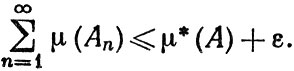
Регулярность функции μ показывает, что множество A содержит элементарное замкнутое множество F, такое, что μ(F)≥μ(A) - ε, а так как множество F компактно, то

при некотором N. Значит,

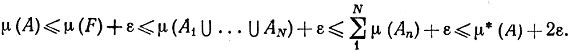
Сопоставляя это неравенство с неравенством (20), получаем утверждение (а).

Пусть теперь Е = ∪ Е_n, и пусть μ^* (Е_n)<+∞ при всех n. Данному числу ε>0 отвечают покрытия {A_nk), k = 1, 2, 3, ..., множеств Е_n открытыми элементарными множествами, такие, что

(21)

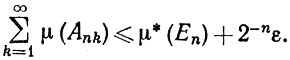
Тогда

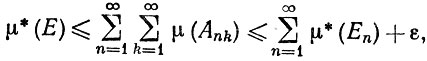
откуда следует (19). Если же μ^* (E_n) = +∞ при некотором n, то неравенство (19), разумеется, тривиально.

10.9.Определение. Для любых множеств A⊂R^p, B⊂R^p положим

(22)

(23)

Будем писать А_n→A, если

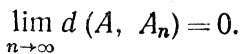
Если существует такая последовательность {А_n} элементарных множеств, что А_n→A, то мы будем говорить, что множество А конечно μ-измеримо, и будем писать А∈_F(μ). Если множество A равно объединению счетного семейства конечно μ-измеримых множеств, то мы будем говорить, что A μ-измеримо, и будем писать A∈(μ).

Множество S (A, В) - это так называемая "симметрическая разность" множеств A и B. Мы увидим, что d (A, В) обладает основными свойствами расстояния.

Следующая теорема позволит нам получить нужное распространение функции μ.

10.10.Теорема. Множество (μ) является σ-кольцом, а функция μ^* счетно-аддитивна на (μ).

Прежде чем обратиться к доказательству этой теоремы, мы изучим некоторые свойства множества S (A, В) и числа d (A, В). Имеем:

(24)

(25)

(26)

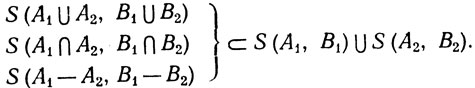
Утверждение (24) очевидно, а (25) следует из того, что

Первая из формул (26) следует из того, что

Наконец, обозначая через Е^с дополнение множества Е, получаем

и последняя из формул (26) получится, если заметить, что

Согласно (23), (19) и (18), из этих свойств множества S (A, B) следует, что

(27)

(28)

(29)

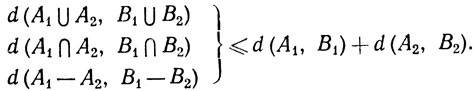
Соотношения (27) и (28) показывают, что d(A, В) удовлетворяет требованиям определения 2.17, за исключением того, что из d(A, B) = 0 не следует А = В. Например, если μ = m, множество A счетно, а B пусто, то

Чтобы убедиться в этом, покроем n-ю точку множества A прямоугольником I_n, таким, что

Но если мы будем считать два множества A и В эквивалентными при условии

то все подмножества пространства R^p разобьются на классы эквивалентности, и d(A, В) превращает множество всех этих классов эквивалентности в метрическое пространство. Тогда _F(μ) оказывается замыканием множества ^*.

^* (Точнее было бы здесь говорить не о _F(μ) и , а о множествах всех классов эквивалентности, содержащих элементы множеств _F(μ) и .- Прим. перев.)

Эта интерпретация несущественна для доказательства, но она объясняет идею, лежащую в его основе.

Нам потребуется еще одно свойство числа d(A, В), а именно

(30)

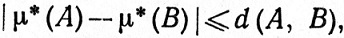
если по крайней мере одно из чисел μ^*(A), μ^*(B) конечно. Действительно, пусть 0≤μ^*(B)≤μ^*(A). Тогда, как показывает неравенство (28),

т. е.

Но так как μ^*(В) конечно, то

Доказательство теоремы 10.10. Пусть А∈_F(μ), B∈_F(μ). Выберем последовательности {А_n}, {В_n} так, чтобы А_n∈, В_n∈, А_n→А, В_n→В. Тогда (29) и (30) показывают, что

(31)

(32)

(33)

(34)

и μ^*(A)<+∞, так как d(A_n, A)→0. Согласно (31) и (33), _F(μ) - кольцо. Согласно (7),

Полагая n→∞, получаем из (34) и теоремы 10.8 (a)

Если А∩B = ∅, то μ^* (А∩B) = 0. Следовательно, функция μ^* аддитивна на _F(μ).

Пусть теперь A∈(μ). Тогда А можно представить в виде объединения счетного множества непересекающихся множеств из _F(μ). Действительно, если A = ∪А'_n, где А'_n∈_F(μ), то положим A₁ = A'₁ и

Тогда

(35)

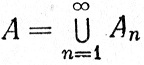
требуемое представление. Согласно (19),

(36)

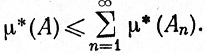
С другой стороны, A⊃А₁∪...∪A_n, и, в силу аддитивности функции μ^* на _F(μ), получаем

(37)

Из (36) и (37) следует, что

(38)

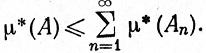
Допустим, что число μ^*(А) конечно. Положим В_n = А₁∪...∪А_n. Тогда, как показывает (38),

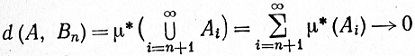
при n→^#8734;. Значит В_n→А, а так как В_n∈_F(μ), то легко видеть, что A∈_F(μ).

Таким образом, мы показали, что A∈_F(μ), если A∈(μ) и μ^*(A)<+∞.

Теперь уже ясно, что функция μ^* счетно-аддитивна на (μ).

Действительно, если

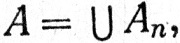
где {А_n} - последовательность непересекающихся множеств, принадлежащих (μ), то, как мы показали, (38) выполняется, если μ^* (А)<+∞ при всех n, а в противном случае равенство (38) тривиально.

Наконец, мы должны показать, что (μ) - это σ-кольцо. Если А_n∈(μ), n = 1, 2, 3, ..., то ясно, что ∪ А_n∈(μ) (теорема 2.14).

Пусть A∈(μ), B∈(μ) и

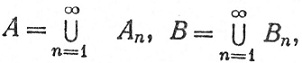
где А_n, В_n∈_F(μ). Тогда тождество

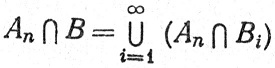
показывает, что А_n∩B∈(μ), а так как

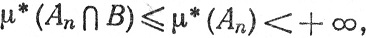
то А_n∩B∈_F(μ) Значит, A_n - B∈_F(μ) и А - B∈(μ), так как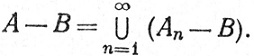

Теперь мы заменим μ^*(А) на μ(A), если A∈(μ). Таким образом, функция μ, определенная первоначально только на , продолжена до счетно-аддитивной функции множества на σ-кольце (μ). Эта продолженная функция множества называется мерой. В том частном случае, когда μ = m (на ), она называется лебеговой мерой в пространстве R^p.

10.11. Замечания.(а) Если множество А открыто, то А∈(μ). Действительно, каждое открытое множество в R^p равно объединению счетного семейства открытых прямоугольников. Чтобы в этом убедиться, достаточно построить счетную базу, элементами которой служат открытые прямоугольники.

(b) Если А∈(μ) и ε>0, то существуют множества F и G, такие, что

F замкнуто, G открыто и

(39)

Первое неравенство выполняется потому, что внешняя мера была определена с помощью покрытий открытыми элементарными множествами. Второе неравенство получится, если перейти к дополнениям.

(c) Мы говорим, что Е - борелевское множество, если Е может быть получено с помощью счетного множества операций, исходя из открытых множеств, причем каждая операция - это либо взятие объединения, либо взятие пересечения, либо переход к дополнению. Множество 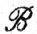всех борелевских подмножеств пространства R^p образует σ-кольцо; в действительности это наименьшее из σ-колец, содержащих все открытые множества. Согласно замечанию (а), Е∈(μ), если E∈.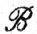

(d) Если А∈(μ), то существуют борелевские множества F и G, такие, что F⊂A⊂G и

(40)

Это следует из (b), если взять ε = ¹/_n и положить n→∞. Поскольку A = F∪(A - F), мы видим, что каждое А∈(μ) представляет собой объединение борелевского множества и множества нулевой меры.

Борелевские множества μ-измеримы при каждом μ. Но множества меры нуль (т. е. множества Е, для которых μ^*(Е) = 0) могут быть различными для различных μ.

(e) Какова бы ни была функция μ, множества меры нуль образуют а-кольцо.

(f) В случае меры Лебега всякое счетное множество имеет меру нуль. Но существуют и несчетные (и даже совершенные) множества меры нуль. Примером может служить множество Кантора: используя обозначения из п. 2.44, легко показать, что

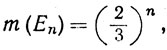
(n = 1, 2, 3, ...),

а так как Р = ∩ Е_n, то Р⊂E_n при любом n, так что m(Р) = 0.

10.12. Определение. Пусть X - множество, не обязательно являющееся подмножеством евклидова пространства или вообще какого-нибудь метрического пространства; X называется пространством с мерой, если существует σ-кольцо подмножеств множества X (элементы множества называются измеримыми множествами) и неотрицательная счетно-аддитивная функция множества μ (называемая мерой), определенная на .

Если, кроме того, Х∈, то X называется измеримым пространством.

Например, мы можем взять в качестве X пространство R^p, в качестве - множество всех измеримых подмножеств пространства R^p, а в качестве μ - меру Лебега.

Или в качестве X можно взять множество всех положительных целых чисел, в качестве - множество всех подмножеств множества X, а в качестве μ(E) - число элементов множества Е.

Другой пример дает теория вероятностей, в которой события можно рассматривать как множества, а вероятность наступления события - это аддитивная (или счетно-аддитивная) функция множества.

В следующих разделах мы всегда будем иметь дело с измеримыми пространствами. Следует подчеркнуть, что теория интеграла, к которой мы вскоре перейдем, ни в каком отношении не стала бы проще, если бы мы пожертвовали той степенью общности, которой мы сейчас достигли, и ограничились, скажем, мерой Лебега на промежутке вещественной прямой. На самом деле основные черты теории с гораздо большей ясностью проявляются именно в общей ситуации, когда хорошо видно, что все зависит только от счетной аддитивности меры μ, определенной на некотором σ-кольце.

Нам будет удобно ввести обозначение

(41)

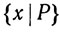
для множества всех элементов х, обладающих свойством Р.