
Функции множества
Пусть А и В - какие-нибудь множества. Символом А-В мы будем обозначать множество всех элементов х, таких, что х∈А, х∉В. Обозначение А-В применяется не только тогда, когда В⊂А. Пустое множество будет обозначаться символом ∅, и мы будем говорить, что множества А и В не пересекаются, если А ∩В = ∅.
10.1.Определение. Множество 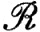 , состоящее из множеств, называется кольцом, если из того, что А∈
, состоящее из множеств, называется кольцом, если из того, что А∈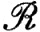 и B∈
и B∈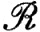 , следует, что
, следует, что
(1)
A∪B∈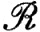 , A-B∈
, A-B∈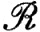
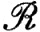 , A-B∈
, A-B∈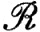
Ввиду того что А∩В = А - (А - В), верно также, что А∩В∈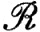 , если
, если 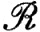 - кольцо.
- кольцо.
Кольцо 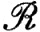 называется σ-кольцом, если
называется σ-кольцом, если
(2)
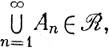
каковы бы ни были множества Аn∈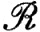 (n = 1, 2, 3, ...). Поскольку
(n = 1, 2, 3, ...). Поскольку
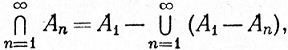
то мы имеем также
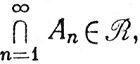
если 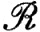 есть σ-кольцо.
есть σ-кольцо.
10.2. Определение. Мы будем говорить, что φ - функция множества, определенная на 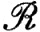 , если φ каждому множеству A∈
, если φ каждому множеству A∈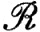 сопоставляет число φ(A), принадлежащее расширенной системе вещественных чисел. Функция φ называется аддитивной, если из того, что А∩В = ∅, А∈
сопоставляет число φ(A), принадлежащее расширенной системе вещественных чисел. Функция φ называется аддитивной, если из того, что А∩В = ∅, А∈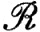 , В∈
, В∈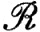 , следует
, следует
(3)
φ(A∪B) = φ(A) + φ(B),
и φ называется счетно-аддитивной, если из того, что Ai∪Aj = ∅ (i≠j), An∈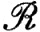 (n = 1, 2, 3, ...), следует
(n = 1, 2, 3, ...), следует
(4)
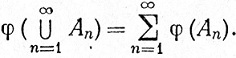
Мы всегда будем предполагать, что не более чем одно из чисел + ∞ и -∞ принадлежит множеству значений функции φ; если бы это было не так, то правая часть равенства (3) могла бы не иметь смысла. Кроме того, мы исключим из рассмотрения функции множества, единственным значением которых служит +∞ или -∞.
Интересно отметить, что левая часть равенства (4) не зависит от порядка, в котором расположены множества Аn. Значит, из теоремы о перестановках ряда следует, что ряд в правой части равенства (4) сходится абсолютно, если вообще сходится; если же он расходится, то его частные суммы стремятся к +∞ или к -∞.
Если функция φ аддитивна, то, как легко видеть, она обладает следующими свойствами:
(5)
φ(∅) = 0,
(6)
φ(A1∪ ... ∪ Аn) = φ(А1) + ... + φ(Аn),
если Ai∩Aj = ∅ при i&38800;j;
(7)
φ(A1∪А2) + φ(A1∩A2) = φ(А1) + φ(А2)
Если φ(A)&38805;0 при всех А и A1 ⊂A2, то
(8)
φ(A1)≤φ(A2)
Имея в виду это неравенство, неотрицательные функции множества часто называют монотонными. Наконец,
(9)
φ(A-B) = φ(A) - φ(B),
если В ⊂А и |φ(В)|< ∞.
10.3. Теорема. Пусть φ-счетно-аддитивная функция множества, определенная на кольце 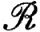 . Пусть Аn∈
. Пусть Аn∈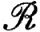 (n = 1, 2, 3, ...), A1⊂A2&38834;А3⊂ ... ⊂А∈
(n = 1, 2, 3, ...), A1⊂A2&38834;А3⊂ ... ⊂А∈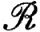 и
и
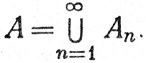
Тогда при n→∞
φ(An)→φ(A)
Доказательство. Пусть A1 = B1 и
Вn = Аn - Аn-1, (n = 2, 3,. ...).
Тогда Bi∩Bj = &38709; при i≠j, An = B1∪...∪Bn и А = ∪Вn. Значит,
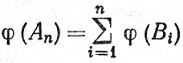
и
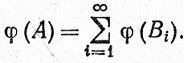
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'