Упражнения

1. Доказать, что каждому A∈L(Rⁿ, R¹) соответствует единственная точка у∈Rⁿ, такая, что Aх = х*у. Доказать, что ||А|| = |у|.

Указание. При некоторых условиях неравенство Шварца превращается в равенство.

2. Доказать, что функция f непрерывна в точке х, если D₁f, ..., D_nf ограничены в некоторой окрестности этой точки.

Указание. Действовать так же, как при доказательстве теоремы 9.16.

3. Пусть f - вещественная дифференцируемая функция на открытом множестве Е⊂Rⁿ, и пусть f имеет локальный максимум в точке х∈Е. Доказать, что f'(х) = 0.

4. Пусть (D₁f)(x) = 0 при всех х из выпуклого открытого множества Е⊂Rⁿ. Доказать, что f(х) зависит только от х₂, ..., х_n. Показать, что выпуклость множества Е можно заменить более слабым условием, но что какое-то условие все-таки требуется. Например, если n = 2, а множество Е имеет форму подковы, то утверждение может и не быть верным.

5. Пусть f - вещественная дифференцируемая функция на связном открытом множестве E⊂Rⁿ, и пусть f'(х) = 0 при всех х∈Е. Доказать, что f постоянна на Е.

6. Вычислить f'(х), если f(х) = |х|² при x∈Rⁿ.

7. Пусть f(0, 0) = 0 и

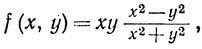
если (х, у)≠(0, 0).

Доказать, что

(a) f, D₁f, D₂f непрерывны на R²;

(b) D₁₂f, D₂₁f существуют в каждой точке пространства R² и непрерывны всюду, кроме точки (0, 0);

(c) (D₁₂f(0, 0) = 1, (D₂₁f)(0,0) = - 1.

8. Из существования (и даже из непрерывности) производной D₁₂f не следует существование производной D₁f. Например, пусть f(x,y) = g(x), где g - нигде не дифференцируемая функция. Тогда D₁f не существует, но D₂f = 0, так что D₁₂f = 0.

9. Положим f(0, 0) = 0 и

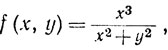
если (x, y) ≠ (0, 0).

Тогда функция f непрерывна в R², а ее сужение на любую прямую дифференцируемо. Более того, покажите что если γ - любая дифференцируемая кривая в R², то функция f (у) дифференцируема. Это значит, что если γ - дифференцируемое отображение сегмента [0, 1] в пространство R² и если g(V) = f(γ(0), то функция g дифференцируема на [0, 1]. Покажите, что если γ∈', то и f(γ)∈'.

Доказать, что, несмотря на это, функция f не дифференцируема в точке (0, 0).

10. Показать, что непрерывность производной f' существенна в теореме об обратной функции, даже в том случае, когда n = 1. Если f(t) = t + 2t²sin(¹/_t) при t ≠ 0, f(0) = 0, то f'(0)≠0, f' ограничена на (- 1, 1), но f не взаимно однозначна ни в какой окрестности точки 0.

11. Пусть f - вещественная дифференцируемая функция на открытом множестве Е⊂Rⁿ. Назовем градиентом функции f в точке х∈E вектор (∇f)(x)∈Rⁿ, такой, что

при всех h∈Rⁿ (ср. с упражнением 1). Если u∈Rⁿ - единичный вектор (т. е. если |u| = 1), то предел

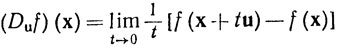
назовем производной функции f в направлении вектора u в точке х.

Доказать, что

и что, стало быть, для любого х∈Е существует вектор u, такой, что

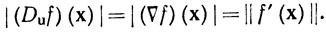
Если (∇f)(x)≠0, то такой вектор u-единственный.

12. Пусть f - отображение, которое точке (x, y)∈R² ставит в соответствие точку (u, v)∈R², где

Каково множество значений отображения f? Показать, что якобиан этого отображения отличен от нуля во всех точках пространства R². Таким образом, каждая точка пространства R² обладает окрестностью, на которой отображение f взаимно однозначно. Тем не менее f не является взаимно однозначным на R².

Каковы образы прямых, параллельных координатным осям, при отображении f?

13. Исследовать аналогичным образом отображение

14. Из системы уравнений

можно х, у, u выразить через z; x, z, u через у; у, z, u через х; но нельзя выразить х, y, z через u.

15. В теореме о неявной функции положить n = m = 1 и истолковать эту теорему графически.

16. Положим f = (f₁, f₂), где

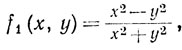
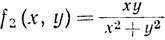
((x, y))≠(0, 0)).

Вычислить ранг преобразования f'(х, у) и найти множество значений отображения f.

17. Переставляющие преобразования B_i действительно нужны в теореме 9.21. Чтобы убедиться в этом, покажите, что отображение (х, у)→(у, х) пространства R² на R² нельзя разложить в произведение двух простых преобразований ни в какой окрестности начала. Найти другие примеры этого явления.

18. Пусть f - то же, что в теореме 9.21. Положим A = f'(0), f₁(x) = A^-1f(x). Тогда f'₁(0) = I. Показать, что

в некоторой окрестности нуля, где g₁, ..., g_n - простые отображения. Таким образом, мы получаем другую теорему о разложении:

19. Пусть φ_i - функция, непрерывная на R¹ (i = 1, 2, 3, ...) с носителем в интервале (2^-i 2^1-i), такая, что ∫ φ_i = 1. Положим

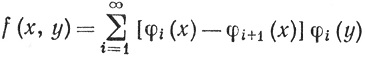
Тогда f имеет компактный носитель, непрерывна всюду, кроме точки (0, 0), и

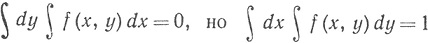
Заметьте, что f не ограничена в каждой окрестности точки (0, 0).

20. Пусть 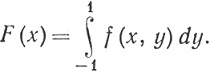. Рассматривая разностные отношения и переходя к пределу, найти условия, при которых

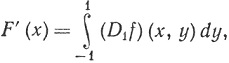
т. е. условия, которые позволяют "дифференцировать под знаком интеграла".

Вот контрпример: при х≥0 положим

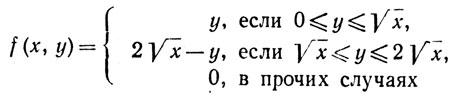
и положим f(-x, -y) = - f(x,y). Тогда функция f непрерывна на R²,

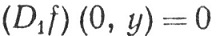
при всех у, но F(x) = x, если |x|<¹/₄.

21. Пусть ω и λ, суть k- и m-формы соответственно. Какова связь между ω∧λ и λ∧ω?

22. Доказать, что каждая k-форма ω в открытом множестве Е⊂Rⁿ может быть приведена к стандартному виду

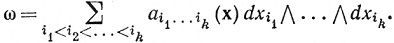
Показать, что если ω = 0, т. е. если 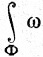= 0 для всех k-поверхностей Φ в Е, то все коэффициенты в этой стандартной записи равны нулю. Показать, что поэтому каждая форма ω единственным образом приводится к стандартному виду.

23. Показать, что (72) можно записать в виде

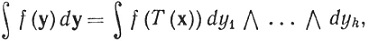
если Т(х) = (у₁, ..., y_k) и если J_T(x)>0.

24. Найти условия, при которых верна формула

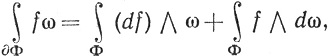
и показать, что ее частным случаем является формула интегрирования по частям.

25. Пусть σ есть k-симплекс (k≥2). Показать, что 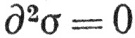, исходя непосредственно из определения граничного оператора 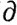. Иными словами, "граница границы" равна нулю. Отметим, что это утверждение согласуется с теоремой Стокса:

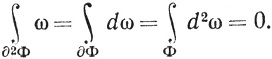
26. Пусть Φ есть k-поверхность с множеством параметров Q^k, пусть Φ^* = Φ(Q_k) - множество значений отображения Φ; если ψ = ∑Φ_i; есть k-цепь, то положим, по определению, ψ^* = ∩Φ^*_i.

Пусть

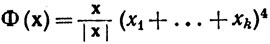
Показать, что Φ - ориентированный симплекс класса " в R^k и что Φ^* заполняет часть замкнутого единичного шара B^k пространства R^k. (Показатель 4 обеспечивает дифференцируемость в начале координат.)

Показать, что существует k-цепь ψ класса " в R^k, такая, что ψ^* = B^k и такая, что (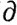ψ)^* - единичная сфера S^k-1, т. е. множество всех x∈R^k, таких, что |x| = 1.

Этот пример показывает, что "-образ прямолинейной цепи вполне может быть "круглым", так что теорема 9.50 применима к разнообразным множествам.

27. Положить k = 3 в упражнении 26 и воспользоваться теоремой Стокса для вычисления интеграла

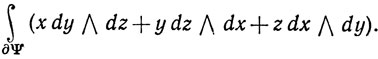
Вычислить при k = 2 интегралы 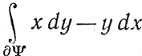и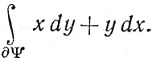

28. Пусть ω = ∑ a_j(х) dx_j есть 1-форма класса ' на открытом множестве Е⊂Rⁿ. Назовем форму ω замкнутой, если dω = 0. Назовем форму ω точной в E, если существует 0-форма f в Е, такая, что ω = df.

(а) Доказать, что ω замкнута тогда и только тогда, когда D_ia_j = D_ja_i при 1≤i≤n, 1≤j≤n.

(b) Доказать, что если ω точна, то ω замкнута.

(с) Пусть множество Е выпукло, а форма ω замкнута. Доказать, что ω точна в Е.

Указание. Зафиксируем p₀∈E, положим f(p) = ∫ ω при p∈ E, где интеграл берется по ориентированному прямолинейному симплексу [p₀, p]. Применить теорему Стокса к прямолинейным 2-симплексам в Ею Показать, что

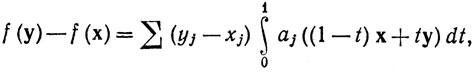
если x∈E, y∈E, и что df = ω.

Таким образом, утверждение, обратное к (b), верно, если множество Е выпукло.

(d) Пусть Т - взаимно однозначное ' - отображение выпуклого открытого множества Е на открытое множество V. Доказать, что каждая замкнутая 1-форма ω в V точна в V.

Указание. Воспользоваться определением 9.41. Согласно (с), ω_Т = df в Е и существует 0-форма g в V, такая, что f = g_T. Тогда ω_T = d(g_T) = (dg)_T, так что ω = dg.

(e) Доказать, что если V - то же, что в (d), если γ - замкнутая '-кривая в V, а ω - замкнутая 1-форма в V, то

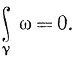
(f) Показать, что утверждения (d) и (e) становятся неверными, если V - пространство R², из которого удалено начало координат, и если

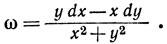
29. Пусть Φ есть 2-поверхность в R³ с множеством параметров D, пусть Ф(u, v) = (x, у, z). Назовем нормалью к поверхности Ф в точке (u, v) вектор

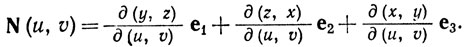
Чем объясняется эта терминология? Если f - функция, непрерывная на Ф^* (см. упражнение 26), то положим

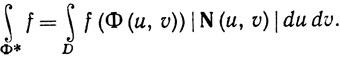
Если f = 1, то этот интеграл называют площадью поверхности Ф. Показать, что определение площади дает естественные результаты в том случае, когда Ф - линейное отображение, когда Ф определяется равенствами

30. Пусть F = (F₁, F₂, F₃) есть ' - отображение открытого множества Е⊂R³ в пространство R³ (в физике такое отображение называют векторным полем). Дивергенция и вихрь (ротор) поля F определяются равенствами

С полем F связаны две дифференциальные формы:

(а) Доказать, что ∇ (∇ *F) = 0, если F∈".

(b) Доказать, что ∇ *F = 0, если F = ∇f при некоторой f∈".

(с) Доказать утверждение, обратное к (b): если V - то же, что в упражнении 28 (d), и если ∇F = 0 в V, то F = ∇f при некоторой f класса " в V.

Указание: F = ∇fΚ означает, что ω = df; связать dω с ∇*F.

(d) Пусть Ψ есть 3-цепь класса " в множестве E, пусть Ф = 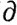Ψ. Применяя к λ теорему Стокса, получить "теорему о дивергенции" Гаусса:

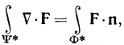
где n = N/|N| в обозначениях упражнения 29.

(е) Пусть Ф есть 2-цепь класса " в множестве Е, и пусть Γ = 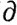Ф. Применяя к ω теорему Стокса, получить формулу

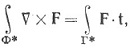
где F*t - "касательная составляющая поля F вдоль Γ". (Мы предоставляем читателю выяснить точный смысл этой последней фразы.)

31. Пусть F = f∇ g, где f и g класса " в открытом множестве E⊂R³. Применяя результат упражнения 30 (d), получить тождество

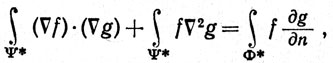
где ∇²g 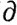= ∇(∇g), g/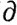n = (∇g)*n, а Ф = 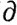Ψ.

(a) Что дает это тождество в том случае, когда f = 1, a g - гармоническая функция (т. е. ∇²g = 0)?

(b) Пусть g гармонична в Е и g = 0 на Φ^*. Полагая в последнем тождестве f = g, доказать, что g = 0 на Ψ^*.