Теорема Стокса

Формулируя эту теорему, мы будем пользоваться терминологией и обозначениями из п. 9.49.

9.50. Теорема. Если Ψ есть k-цепь класса " в открытом множестве V⊂R^m и если ω есть (k-1)-формa класса ' в V, то

(100)

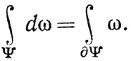
(В случае k = m = 2 эту теорему называют теоремой Грина. В случае k = m = 1 эта теорема - не что иное, как основная теорема интегрального исчисления.)

Доказательство. Достаточно доказать, что

(101)

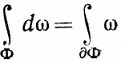
для каждого ориентированного k-симплекса Φ класса " в V, так как если доказано (101), а Ψ = ∑ Φ_i, то из (99) следует, что (100) тоже выполняется.

Зафиксируем такое Φ, и пусть σ - ориентированный прямолинейный k-симплекс в R^k:

(102)

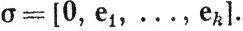
Этот симплекс σ - просто тождественное отображение на Q^k; в обозначениях (92) здесь р₀ = 0, A = I.

Ввиду того что Φ - класса " в V, существует открытое множество Е⊂R^k, содержащее Q^k, и "-отображение Т множества Е в V, такое, что Φ = T(σ). Левая часть равенства (101) равна

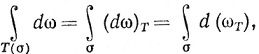
согласно теоремам 9.45 и 9.42 (с). Еще раз применяя 9.45, мы видим, что правую часть равенства (101) можно записать в следующем виде:

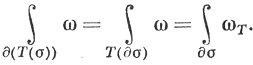
Таким образом, достаточно доказать, что

(103)

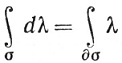
для специального симплекса (102) и произвольной (k-1)-формы класса ' в Е.

Граница симплекса (102) равна

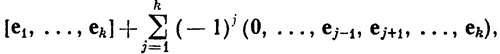
согласно (96). Передвинем элемент 0 в j-м слагаемом этой суммы так, чтобы он оказался между e_j-1 и e_j+1. Это можно сделать с помощью j-1 транспозиций. Значит,

(104)

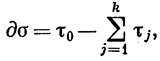
где τ₀ = [e₁, ..., е_k] и τ_j получается из τ₀ заменой е_j на 0, j = 1, ..., k.

Если k = 1, то из определения ориентированного 0-симплекса вытекает, что в (103) утверждается всего лишь следующее:

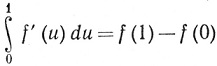
для любой непрерывно дифференцируемой функции f на [0, 1]; это утверждение справедливо, согласно основной теореме интегрального исчисления.

Если k>1, то достаточно доказать (103) для

(105)

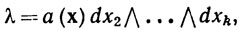
где a∈'(E), так как (104) показывает, что то же самое будет тогда справедливо и для любой формы αβ^k-1, а любая (k-1)-форма равна сумме форм вида αβ^k-1.

Множеством параметров для симплексов τ₀, ..., τ_k служит симплекс Q^k-1. Если u = (u₁, ..., u_k-1)∈Q^k-1, а х = (x₁, ..., x_k) = τ₀(u), то

(106)

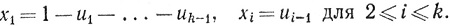
Если х = τ₁(u), то

(107)

Если х = τ_j(u) и 2≤j≤k, то x_j = 0. Следовательно, якобиан

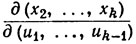
равен 1 для τ₀ и τ₁ и равен нулю для τ₂, ..., τ_k. Таким образом,

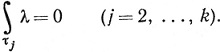
Отсюда будет следовать (103) после того, как мы покажем, что

(108)

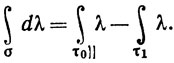
Левая часть равенства (108) равна

(109)

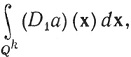
так как 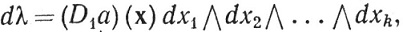, a σ - тождественное отображение на Q^k.

Вычисляя k-кратный интеграл (109) интегрированием по x₁, получаем

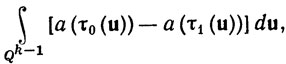
согласно (106) и (107), что в свою очередь равно правой части равенства (108). Теперь доказательство закончено.