
Симплексы и цепи
9.46. Определения. При k = 1, 2, 3, ... мы определяем стандартный симплекс Qk как множество всех u∈Rk вида
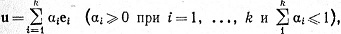
где {е1, ..., ek} - стандартный базис пространства Rk.
Если р0, р1, ..., pk - точки пространства Rn и А - линейное отображение пространства Rk в пространство Rn, определяемое равенствами Aеi = рi-р0 (i = 1, ..., k), то ориентированным прямолинейным k-симплексом
(91)
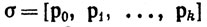
называется k-поверхность в Rn с множеством параметров Qk, заданная равенством
(92)
σ(u) = p0 + Au (u∈Qk).
Заметим, что σ(0) = р0, σ(еi) = рi при i = 1, ..., k.
Мы называем симплекс σ ориентированным, чтобы подчеркнуть, что порядок вершин р0, ..., pk следует учитывать. Если
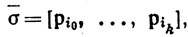
где {i0, i1, ..., ik) - перестановка множества {0, 1, ..., k}, то мы будем писать
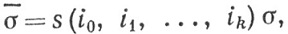
где s-функция, определенная в п. 9.22. Таким образом, 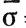 = ±σ в зависимости от того, какое из двух равенств s = 1 или s = - 1 выполняется. Строго говоря, считая (91) и (92) определением симплекса σ, мы имеем право писать
= ±σ в зависимости от того, какое из двух равенств s = 1 или s = - 1 выполняется. Строго говоря, считая (91) и (92) определением симплекса σ, мы имеем право писать 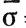 = σ только в том случае, когда i0 = 0, ..., ik = k, хотя бы s(i0, ..., ik) и равнялось 1, так что, строго говоря, здесь мы имеем дело не с равенством, а с отношением эквивалентности. Однако для наших целей такое обозначение оправдано, как показывает теорема 9.47.
= σ только в том случае, когда i0 = 0, ..., ik = k, хотя бы s(i0, ..., ik) и равнялось 1, так что, строго говоря, здесь мы имеем дело не с равенством, а с отношением эквивалентности. Однако для наших целей такое обозначение оправдано, как показывает теорема 9.47.
Если 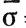 = εσ (мы следуем только что принятому соглашению) и если ε = 1, то говорят, что
= εσ (мы следуем только что принятому соглашению) и если ε = 1, то говорят, что 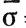 и σ имеют одинаковую ориентацию; если ε = - 1, то говорят, что
и σ имеют одинаковую ориентацию; если ε = - 1, то говорят, что 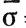 и σ имеют противоположные ориентации. Заметим, что мы не определяем, что такое "ориентация симплекса". То, что мы определили - это отношение между парами симплексов, имеющих одно и то же множество вершин, т. е. свойство двух таких симплексов иметь одинаковую ориентацию.
и σ имеют противоположные ориентации. Заметим, что мы не определяем, что такое "ориентация симплекса". То, что мы определили - это отношение между парами симплексов, имеющих одно и то же множество вершин, т. е. свойство двух таких симплексов иметь одинаковую ориентацию.
До сих пор мы предполагали, что k≥1. Ориентированным 0-симплексом называется точка, которой приписан некоторый знак. Мы пишем σ = + p0 или σ = - р0. Если σ = εр0 (ε = ± 1) и если f есть 0-форма (т. е. вещественная функция), то мы полагаем, по определению,
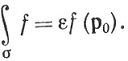
9.47. Теорема. Если σ-ориентированный прямолинейный k-симплекс в открытом множестве Е⊂Rn и если 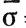 = εσ, то
= εσ, то
(93)
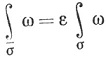
для любой k-формы ω в Е.
Доказательство. Если k = 0, то (93) следует из предыдущего определения. Итак, будем считать, что k≥1 и что σ - симплекс (91).
Пусть 1<j≤k, и пусть 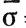 получается из σ перестановкой вершин р0 и рj. Тогда ε = -1 и
получается из σ перестановкой вершин р0 и рj. Тогда ε = -1 и
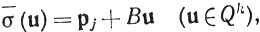
где В - линейное отображение пространства Rk в пространство Rn, определенное равенствами Bеj = р0 - рj, Веi = рi - рj, если i≠j.
Обозначая Aеi = xi (1≤i≤k), где А задано равенствами (92), мы видим, что столбцы матрицы [В] (т. е. векторы Bei) таковы
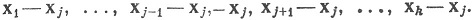
Если вычесть из каждого столбца j-й столбец, то ни один из определителей в (76) не изменится, и мы получим столбцы х1, ..., xj-1, - xj+1, ..., xk. Они отличаются от соответствующих столбцов матрицы [А] только знаком j-го столбца. Значит, в этом случае (93) доказано.
Пусть теперь 0<i<j≤k и пусть 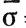 получается из σ перестановкой вершин рi и рj. Тогда
получается из σ перестановкой вершин рi и рj. Тогда 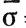 (u) = p0 + Cu, где [С] имеет те же столбцы, что и [А], за исключением i-гo и j-го, которые переставлены. Отсюда снова следует, что выполняется (93), так как ε = - 1.
(u) = p0 + Cu, где [С] имеет те же столбцы, что и [А], за исключением i-гo и j-го, которые переставлены. Отсюда снова следует, что выполняется (93), так как ε = - 1.
Поэтому (93) выполняется и в общем случае, так как каждая перестановка множества {0, 1, ..., k} равна суперпозиции перестановок, с которыми мы уже имели дело.
9.48. Определение.Прямолинейной k-цепью Γ в открытом множестве Е⊂Rn называется семейство, состоящее из конечного числа ориентированных k-симплексов σ1, ..., σr в Е (не обязательно различных).
Если Γ - такая цепь и если ω есть k-форма а Е, то, по определению, полагаем
(94)
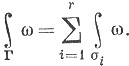
Мы можем рассматривать k-поверхность Φ в Е как функцию, определенную на множестве всех k-форм ω в Е, сопоставляющую каждой форме ω число 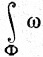 . Вещественные функции можно складывать (см. определение 4.3), поэтому (94) подсказывает следующее обозначение:
. Вещественные функции можно складывать (см. определение 4.3), поэтому (94) подсказывает следующее обозначение:
(95)
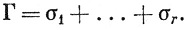
Например, если σ2 = - σ1 и Γ = σ1 + σ2, то 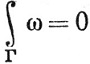 при всех ω. В этом случае можно записать Г = 0.
при всех ω. В этом случае можно записать Г = 0.
При k = 1, 2, 3, ... границей ориентированного прямолинейного k-симплекса σ = [р0, p1, ..., pk] называется прямолинейная (k-1)-цепь
(96)
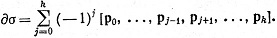
Например, если σ = [р0, p1, р2], то
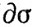 = [p1, р2] - [p0, р2] + [p0, р1] = [p0, р1] + [p1, р2] + [p2, р0].
= [p1, р2] - [p0, р2] + [p0, р1] = [p0, р1] + [p1, р2] + [p2, р0].Это совпадает с обычным определением ориентированной границы треугольника.
Заметим, что если 1≤j≤k, то симплекс σj = [р0, ..., рj-1, рj+1, ..., pk], фигурирующий в (96), имеет Qk-1 своим множеством параметров, и что он определяется так:
(97)
σj(u) = p0 + Bu (u∈Qk-1),
где B - линейное отображение из Rk-1 в Rn, определяемое равенствами
Bei = pi - p0,
если 1≤i≤j-1, Bei = pi+1 - p0, если j≤i≤k-1. Симплекс
σ0 = [р1, p2, ..., рk]
который тоже участвует в (96), задается как отображение
σ0(u) = p1 + Bu,
где Bei = pi+1 - p1 при 1≤i≤k-1.
9.49. Определение. Пусть Т есть  "-отображение открытого множества E⊂Rn в открытое множество V⊂Rm, не обязательно взаимно однозначное. Если σ - ориентированный прямолинейный k-симплекс в E, то сложное отображение Φ = Т(σ) есть k-поверхность в V с множеством параметров Qk. Мы будем называть Φ ориентированным k-симплексом класса
"-отображение открытого множества E⊂Rn в открытое множество V⊂Rm, не обязательно взаимно однозначное. Если σ - ориентированный прямолинейный k-симплекс в E, то сложное отображение Φ = Т(σ) есть k-поверхность в V с множеством параметров Qk. Мы будем называть Φ ориентированным k-симплексом класса  ".
".
Конечное семейство Ψ ориентированных k-симплексов Φ1, ..., Φr класса  " в V называется k-цепью класса
" в V называется k-цепью класса  " в V; если ω есть k-форма в V, то, по определению, полагаем
" в V; если ω есть k-форма в V, то, по определению, полагаем
(98)
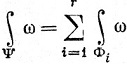
и используем соответствующее обозначение Ψ = ∑ Φi. Если Γ = ∑ σi - прямолинейная цепь и Φi = Γ(σi), то мы будем писать Ψ = T(Γ), или
Граница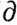 Φ ориентированного k-симплекса Φ = Т (σ) - это, по определению, (k-1)-цепь
Φ ориентированного k-симплекса Φ = Т (σ) - это, по определению, (k-1)-цепь
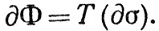
Очевидно, что 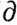 Φ принадлежит классу
Φ принадлежит классу  ", если Φ принадлежит этому классу.
", если Φ принадлежит этому классу.
Наконец, мы определяем границу 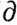 Ψ некоторой k-цепи Ψ = ∑ Φi как (k-1)-цепь
Ψ некоторой k-цепи Ψ = ∑ Φi как (k-1)-цепь
(99)
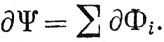
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'