Дифференциальные формы

В этом разделе будет частично разработан аппарат, необходимый для теоремы Стокса.

До сих пор мы рассматривали производные функций нескольких переменных только для функций, определенных на открытых множествах. Это было вызвано соображениями удобства и позволило нам избежать трудностей, которые могут встретиться при рассмотрении граничных точек. Однако теперь нам будет удобно рассматривать дифференцируемые функции на компактных множествах. Поэтому мы примем следующее соглашение. Говоря, что f есть 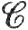'-отображение (или 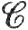"-отображение) компактного множества D⊂R^k в пространство Rⁿ, мы будем иметь в виду, что существует 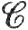'-отображение (или 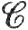"-отображение) g некоторого открытого множества W⊂R^k в пространство Rⁿ, такое, что D⊂W и g(x) = f(x) при всех x∈D.

9.35. Определение. Пусть Е - открытое множество в Rⁿ; '-отображение Φ некоторого компактного множества D⊂R^k в множество Е мы будем называть k-поверхностью в множестве Е.

Множество D называется множеством параметров поверхности Φ. Точки множества D мы будем обозначать через u, так что u = (u₁, ..., u_k).

Мы будем иметь дело только с простейшей ситуацией, когда D- или k-клетка, или k-симплекс Q^k, описанный в примере 9.31. Причина этого в том, что нам предстоит интегрировать по D, а мы еще не развили теории интегрирования по более сложным подмножествам пространства R^k. Мы увидим, что это ограничение, наложенное на D (мы будем его в дальнейшем, не оговаривая, предполагать выполненным) не влечет существенной потери общности в теории дифференциальных форм.

Сравнение с определением 6.34 показывает, что 1-поверхность - это не что иное, как непрерывно дифференцируемая кривая.

9.36. Определение. Пусть Е - открытое множество в пространстве Rⁿ. Дифференциальной формой порядка k≥1, определенной в Е(или, кратко, k-формой в Е) называется функция ω на множестве k-поверхностей, символически записываемая в виде

(75)

oннлексы i₁, ..., i_k независимо пробегают множество 1, ..., n) и сопоставляющая каждой k-поверхности Φ в множестве Е число 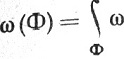в соответствии с правилом

(76)

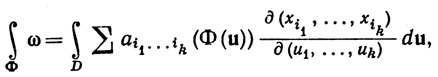
где D - множество параметров поверхности Φ.

Функции a_i1 ... _ik предполагаются вещественными и непрерывными в Е. Если φ₁, ..., φ_n - компоненты отображения Φ, то якобиан в (76) - это якобиан отображения

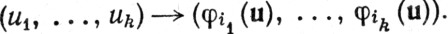
Заметим, что правая часть равенства (76) - интеграл по множеству А описанный в п. 9.28 (или 9.31), и что (76) - определение символа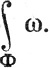

Говорят, что k-форма ω принадлежит классу 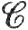' или 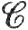", если функции a_i1 ... _ik в (75) принадлежит классу 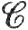' или ".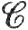

0-формой называют функцию, непрерывную на множестве Е.

Формы (77)

называют базисными k-формами. Чтобы упростить обозначения, мы часто будем употреблять символ β^k только для базисных k-форм. Каждая k-форма оказывается тогда суммой k-форм fβ^k, где f есть 0-форма.

В качестве простого примера рассмотрим 1-поверхность γ в R² (т. е. кривую класса 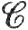') с множеством параметров [0, 1]. Если ω = x₂ dx₁ + x₁ dx₂, то

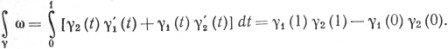
Если γ - замкнутая кривая, то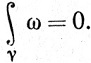

9.37. Элементарные свойства k-форм. Пусть ω, ω₁, ω₂ суть k-формы в Е. Мы будем писать ω₁ = ω₂ тогда и только тогда, когда ω₁(Φ) = ω₂(Φ), какова бы ни была k-поверхность Φ в множестве Е; в частности, ω = 0 означает, что ω(Φ) = 0 для всех k-поверхностей Φ в множестве Е. Если с - вещественное число, то cω есть k-форма, определенная равенством

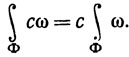
В частности, - ω определяется так, что

(78)

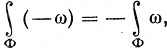
и ω = ω₁ + ω₂ означает, что

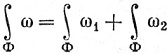
для всех k-поверхностей Φ в множестве Е.

Согласно (78) и (76), из того, что определитель меняет знак при перестановке двух его столбцов, следует, что выполняется антикоммутативный закон

(79)

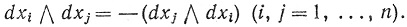
Полагая в (79) i = j, получаем

(80)

последовательно, каждая k-форма от n переменных - нулевая, если k>n.

9.38. Умножение. Пусть ω есть k-форма (75), а λ есть m-форма

(81)

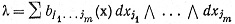
в Е, где j₁, ..., j_m независимо пробегают множество целых чисел от 1 до n. Произведение этих форм, обозначаемое символом ω∧ λ, есть, по определению, (k + m)-форма

(82)

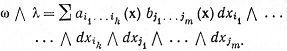
В сумме (82) индексы i₁, ..., i_k, j₁, ..., j_m изменяются независимо от 1 до n.

Определенное так умножение, очевидно, ассоциативно и дистрибутивно по отношению к сложению, определенному в разделе 9.37. Заметим, что ранее введенное обозначение

согласуется с нашим теперешним определением умножения.

9.39. Дифференцирование. Мы определим теперь оператор дифференцирования d, который каждой k-форме класса 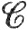' в множестве Е ставит в соответствие (k + 1)-форму в Е.

0-форма класса 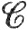' в Е - это просто вещественная функция f∈'(E), и мы полагаем, по определению,

(83)

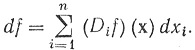
Если ω - fβ^k, где β^k - базисная k-форма, то ее производной dω называется (k + 1)-форма

(84)

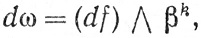
где df - то же, что в (83), а произведение понимается в смысле п. 9.38. Оператор d распространяется на суммы членов fβ^k (т. е. на все k-формы ω) по аддитивности.

Часто форму dω называют внешней производной формы ω, а ω∧λ называют внешним произведением форм ω и λ. В соответствии с этим формальное исчисление, построением которого мы сейчас занимаемся, называют внешним дифференциальным исчислением.

9.40. Теорема.(а) Если ω и λ суть k- и m-формы (соответственно) класса ' в Е, то

(85)

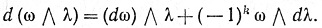
(b) Если ω - форма класса 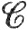" в Е, то d²ω = 0 в Е. Здесь d²ω обозначает, разумеется, форму d(dω).

Доказательство. Для доказательства равенства (85) достаточно рассмотреть частный случай ω = fβ^k, λ = gβ^m где f, g∈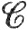'(E), a β^k, β^m - базисные формы. Тогда

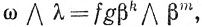
так что

(86)

Согласно (83),

(87)

Соотношение антикоммутативности (79) показывает, что

(88)

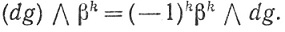
Согласно (88), подставляя (87) в (86), получаем (85). Если f есть 0-форма класса 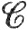", то

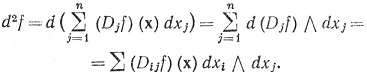
Ввиду того что D_ijf = D_jif и dx_i∧dx_j = - dx_j∧dx_i, мы видим, что d²f = 0. Если ω = fβ^k, то dω = (df) ∧β^k, а так как d(β^k) = 0, то из (85) следует, что d²ω = (d²f) ∧β^k = 0.

9.41. Определение. Пусть Е - открытое множество в пространстве Rⁿ, Т есть 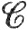'-отображение множества Е на открытое множество V⊂R^m, а ω есть k-форма в V:

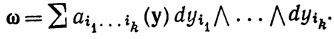
Тогда T преобразует форму ω в k-форму ω_T в Е, заданную следующим образом:

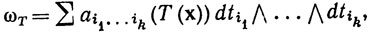
где t₁, ..., t_m - компоненты отображения T; другими словами, если (у₁, ..., y_m) = T(x), то y_i = t_i(x) и в соответствии с (83)

Наша следующая теорема показывает, что операции сложения, умножения и дифференцирования форм определены так, что они инвариантны относительно замены переменных.

9.42. Теорема.Пусть Е и Т - те же, что в определении 9.41. Пусть ω и λ суть k- и m-формы (соответственно) в V. Тогда

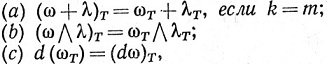
если ω-класса 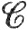', а Т - класса ".

Доказательство.(а) и (b) вытекают непосредственно из определений. Если f есть 0-форма класса ' в V, то

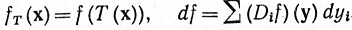
Из правила дифференцирования следует, что

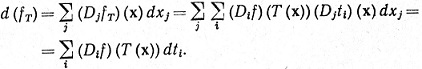
Таким образом,

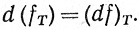
Допустим, теперь, что ω = fβ^k, где β^k = dy_i1∧... ∧dy_ik. Тогда (β^k)_T = dt_i ∧... ∧dt_ik и из теоремы 9.40 следует, что d((β^k)_T) = 0 (это единственное место, где мы используем предположение о том, что Т∈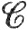"). Поскольку

то (85) и (b) показывают теперь, что

Тем самым доказано и (с).

Теперь мы переходим к другому важному свойству преобразований дифференциальных форм.

9.43. Теорема. Пусть Т есть 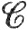'-отображение открытого множества Е⊂Rⁿ в открытое множество V⊂R^m, S есть 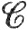'-отображение множества V в открытое множество W⊂R^p, а ω является k-формой в W, так что ω_S есть k-форма в V, и обе формы (ω_S)_T и ω_ST суть k-формы в Е, где ST определяется равенством (ST)(х) = S(Т(x)). Тогда

Доказательство. Если ω и λ - формы в W, то, как показывает теорема 9.42,

и

Таким образом, если (89) выполняется для ω и для λ, то (89) выполняется и для ω ∧λ. Поскольку каждую форму можно построить из 0-форм и 1-форм с помощью операций сложения и умножения и поскольку (89) выполняется тривиальным образом для 0-форм, то достаточно доказать (89) в том случае, когда ω = dz_q, q = 1, ..., p. (Мы обозначаем точки множеств Е, V, W через х, у, z соответственно.)

Пусть t₁, ..., t_m - компоненты отображения Т, s₁, ..., s_p - компоненты отображения S, а r₁, ..., r_р - компоненты отображения ST. Если ω = dz_q, то

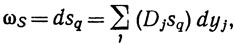
так что по правилу дифференцирования (см. пример 9.14)

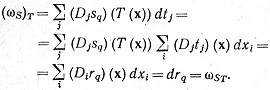
9.44. Теорема. Пусть ω есть k-форма в открытом множестве Е∈Rⁿ, Φ есть k-поверхность в Е с множеством параметров D∈R^k, а Δ есть k-поверхность в R^k с множеством параметров D, определенная так: Δ(u) = u(u∈D). Тогда

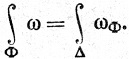
Доказательство.Нам достаточно рассмотреть только случай

Если φ₁, ..., φ_n - компоненты отображения Φ, то

Теорема будет доказана, если мы установим, что

(90)

где

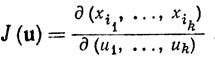
поскольку из (90) следует, что

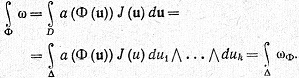
Пусть [А] - матрица из k строк и k столбцов с элементами

Тогда

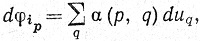
так что

В последней сумме q₁, ..., q_k изменяются независимо от 1 до k. Из закона антикоммутативности (79) следует, что

где s - то же, что в определении 9.22. Применяя это определение, мы видим, что

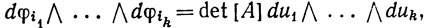
а так как J(u) = det [А], то (90) доказано.

Комбинируя две последние теоремы, получаем заключительный результат этого раздела.

9.45. Теорема. Пусть Т есть 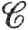'-отображение открытого множества Е⊂Rⁿ в открытое множество V⊂R^m, Φ есть k-поверхность в Е, а ω есть k-форма в V. Тогда

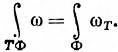
Доказательство. Пусть D - множество параметров поверхности Ф (и тем самым поверхности ТФ). Определим Δ, как в теореме 9.44. Применяя эту теорему к ω_T и Ф, получаем

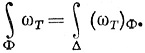
Применяя этот результат к ω и к TФ, получаем

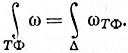
Но (ω_T)_Φ = ω_TΦ по теореме 9.43. Теорема доказана.