
Интегрирование
9.28. Определение. Назовем k-клеткой (или k-мерной клеткой) множество Ik⊂Rk, состоящее из точек х = (x1, ..., xk), для которых
(67)
ai≤xi≤bi (i = 1, ..., k).
Пусть f - непрерывная вещественная функция на Ik. Положим fk = f, и пусть
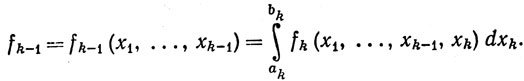
Из равномерной непрерывности функции fk на Ik следует, что fk-1 - непрерывная функция на множестве Ik-1, т. е. (k-1) - клетке в пространстве Rk-1, определяемой первыми k-1 неравенствами из (67). Поэтому мы можем продолжить процесс. В результате для каждого j, 1≤j≤k, мы получим непрерывную функцию fj на клетке Ij⊂Rj причем fj-1 есть интеграл от fj относительно xj по сегменту [аj, bj]. Наконец, проинтегрировав f1, мы получим
число f0, которое называется интегралом функции f no k-клетке Ik и записывается в виде
(68)
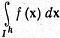
или
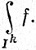
На первый взгляд это определение интеграла зависит от порядка, в котором производятся k однократных интегрирований. Однако это только кажущаяся зависимость. Чтобы доказать это, введем временно обозначение L(f) для интеграла (68) и L'(f) - для интеграла, возникающего в результате k интегрирований, произведенных в каком-либо ином порядке.
9.29. Теорема. Какова бы ни была функция f∈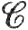 (Ik), имеем L (f) = L'(f).
(Ik), имеем L (f) = L'(f).
Доказательство. Если h (x) = h1(х1)... hk(xk), где hj∈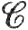 ([aj,bj]), то
([aj,bj]), то
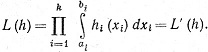
Если Α - множество всех конечных сумм таких функций h, то L(g) = L'(g) при всех g∈Α. Кроме того, Α - алгебра функций на множестве Ik, к которой применима теорема Стона-Вейерштрасса.
Положим 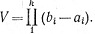 Если f∈
Если f∈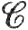 (Ik), a ε>0, то существует функция g∈Α, такая, что ||f-g||<ε/V, где ||f|| = max|f(x)|(x∈Ik). Тогда |L(f-g)|<ε, |L'(f-g)|<ε, и так как
(Ik), a ε>0, то существует функция g∈Α, такая, что ||f-g||<ε/V, где ||f|| = max|f(x)|(x∈Ik). Тогда |L(f-g)|<ε, |L'(f-g)|<ε, и так как
L(f)-L'(f) = L(f-g)+L'(g-f),
то |L(а)-L'(а)|<2ε. Тем самым теорема доказана. С этим пунктом связано упражнение 19.
9.30. Определение.Носителем (вещественной или комплексной) функции f, определенной на Rk, называется замыкание множества всех точек x∈Rk, в которых f(х)≠0. Если f - непрерывная функция с компактным носителем, a Ik - какая-нибудь k-клетка, содержащая носитель функции f, то положим
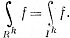
Так определенный интеграл, очевидно, не зависит от выбора Ik, лишь бы клетка Ik содержала носитель функции f.
Может показаться заманчивым распространить это определение интеграла по пространству Rk на функции, которые служат пределами (в некотором смысле) непрерывных функций с компактными носителями. Мы не хотим обсуждать условия, при которых это можно сделать; этот вопрос уместно решать с помощью интеграла Лебега. Мы лишь опишем один очень простой пример, который будет использован при доказательстве теоремы Стокса.
9.31. Пример. Пусть Qk есть k-симплекс, состоящий из всех точек х = (х1, ..., xk) пространства Rk, таких, что x1 + ... +xk≤1 и xi≥0 при i = 1, ..., k. Если k = 3, например, то Qk - это тетраэдр с вершинами 0, е1, е2, е3. Если f∈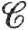 (Qk), то продолжим функцию f до функции, определенной на единичном кубе Ik, полагая f(х) = 0 вне Qk.
(Qk), то продолжим функцию f до функции, определенной на единичном кубе Ik, полагая f(х) = 0 вне Qk.
Если полученная в результате продолжения функция окажется непрерывной, то естественно положить
(69)
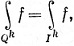
причем интеграл справа в этой формуле определяется в соответствии с п. 9.28.
Однако в общем случае продолженная функция будет разрывной на Ik, и нам следует определить правую часть в (69). Мы сейчас покажем, как это можно сделать. Конечно, мы можем действовать так же, как в п. 9.28, и в этом случае необходимо установить, что интеграл не зависит от порядка, в котором выполняются k однократных интегрирований. Приводимое ниже рассуждение заодно содержит доказательство и этого факта.
Положим y = (x1, ..., xk-1), x = (y, xk). Определим функцию g:g(x) = f(x) при x∈Qk, g(x) = f(x/t), если x1 + ... + xk = t>1, и положим
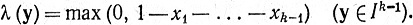
Действуя в соответствии с определением 9.28, получим
(70)
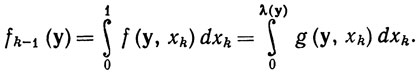
Поскольку g∈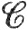 (Ik), а λ∈
(Ik), а λ∈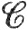 (Ik-1), то из (70) следует, что fk-1∈
(Ik-1), то из (70) следует, что fk-1∈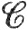 (Ik-1). Значит, последующие интегрирования не составляют проблемы.
(Ik-1). Значит, последующие интегрирования не составляют проблемы.
Если 0<ε<1, то положим φ(t) = 1 при t<1-ε, φ(t) = (1 - t)/ε на сегменте [1-ε, 1], φ(t) = 0 при t>1, и пусть
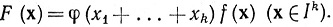
Тогда 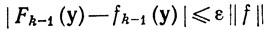 при всех у∈Ik-1, так что
при всех у∈Ik-1, так что
(71)
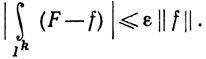
Отметим, что неравенство (71) справедливо вне зависимости от порядка, в котором производятся k однократных интегрирований; ввиду того что F∈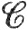 (Ik), на интеграле ∫F не сказывается никакое изменение этого порядка; (71) показывает, что то же верно и в отношении ∫f.
(Ik), на интеграле ∫F не сказывается никакое изменение этого порядка; (71) показывает, что то же верно и в отношении ∫f.
Наша следующая теорема показывает, как действует на интеграл замена переменных. Для простоты мы ограничимся непрерывными функциями с компактным носителем.
9.32. Теорема. Пусть Т - взаимно однозначное 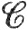 ' - отображение открытого множества Е⊂Rk в пространство Rk, такое, что JT(х)≠0 при всех х∈Е. Если f - непрерывная функция на Rk с компактным носителем, содержащимся в Т(Е), то
' - отображение открытого множества Е⊂Rk в пространство Rk, такое, что JT(х)≠0 при всех х∈Е. Если f - непрерывная функция на Rk с компактным носителем, содержащимся в Т(Е), то
(72)
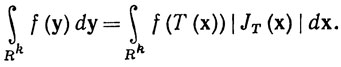
Напомним, что JT - якобиан отображения Т. Так как JT(x)≠0, то по теореме об обратной функции отображение Т-1 непрерывно на множестве Т(Е), и тем самым подинтегральная функция в правой части равенства (72) имеет компактный носитель, содержащийся в Е (теорема 4.14).
Поясним появление абсолютной величины якобиана JT(x) в (72). Пусть k = 1. Предположим, что Т - взаимно однозначное 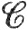 '-отображение пространства R1 на R1. Тогда JT(x) = T'(x). Если Т возрастает, то, согласно теоремам 6.33 и 6.17, какова бы ни была непрерывная функция f с компактным носителем,
'-отображение пространства R1 на R1. Тогда JT(x) = T'(x). Если Т возрастает, то, согласно теоремам 6.33 и 6.17, какова бы ни была непрерывная функция f с компактным носителем,
(73)
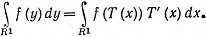
(Здесь можно обойтись и теоремой 6.16, так как функция T' непрерывна.) Но если Т убывает, то Т'(х)<0, и если функция f положительна на внутренности своего носителя, то правая часть равенства (73) отрицательна, а левая положительна. Верное равенство получится, если T' заменить в (73) на |Т'|.
Заметим, что интегралы, которые мы сейчас рассматриваем,- это интегралы от функций по подмножествам пространства Rk, и с этими подмножествами мы не связываем никакой ориентации или направления. Мы встанем на другую точку зрения, когда будем заниматься интегрированием дифференциальных форм по поверхностям.
Доказательство. Из только что сделанных замечаний следует, что (72) справедливо, если Т - простое  '-отображение (см. теорему 9.21), а теорема 9.29 показывает, что (72) верно и в том случае, когда T - линейное преобразование, меняющее местами две координаты.
'-отображение (см. теорему 9.21), а теорема 9.29 показывает, что (72) верно и в том случае, когда T - линейное преобразование, меняющее местами две координаты.
Если теорема верна для отображений Р, Q и если S(x) = P(Q (x)), то
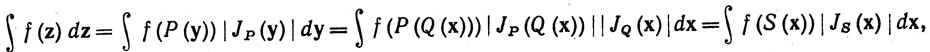
так как
JP(Q (х))JQ(x) = det P'(Q (x))det Q'(x) = det P'(Q (x))Q'(x) = det S'(x) = JS (x),
согласно теореме об умножении определителей и правилу дифференцирования сложной функции. Таким образом, теорема верна и для S.
Каждая точка а∈E имеет окрестность U, в которой
T(x) = T(a) + gk(Bkgk-1(...g1(B1(x-a)))),
где gi, Bi те же, что в теореме 9.21. Полагая V = T(U), получаем, что (72) справедливо, если носитель функции f содержится в V. Итак:
Каждая точка множества Т (Е) имеет окрестность V, такую, что (72) справедливо для любой непрерывной функции f с носителем, содержащимся в V.
Теперь пусть f - непрерывная функция с компактным носителем К, содержащимся в Т(Е). Каждая точка у∈К служит центром некоторого открытого шара V(y) радиуса r(у), такого, что (72) выполняется для каждой непрерывной функции с носителем, лежащим в V(y). Поскольку множество К компактно, существуют точки у1, ..., уp, принадлежащие К и такие, что объединение открытых шаров Wi с центром yi и радиуса 1/2 r(yi) покрывает К.
Пусть βi(1≤i≤p) - функция, непрерывная на Rk, с носителем в V (уi), такая, что βi(y) = 1 на Wi. Положим α1 = β1 и
αj = (1 - β1)(1 - β2)...(1 - βj-1)βj,
если 2≤j≤р. Легко проверить, что
α1 + ... +αp = 1 - (1 - β1)(1 - β2)...(1 - βp)
В каждой точке множества К обращается в нуль хотя бы один из сомножителей последнего произведения, так что ∑αi(y) = 1, если у∈K. Носитель непрерывной функции αjf лежит в V(yj), так что (72) выполняется при каждом αjf. Из равенства f = ∑ αjf следует, что (72) справедливо и для f.
9.33. Определение. Пусть f - вещественная функция, определенная на открытом множестве Е⊂Rn, с частными производными D1f, ..., Dnf (см. п. 9.13). Если функции Djf сами дифференцируемы, то частные производные второго порядка функции f определяются равенством
Dijf = DiDjf (i,j = 1, ..., n).
Если все эти функции Dijf непрерывны на E, то говорят, что f - функция класса  " на Е или что f∈
" на Е или что f∈ "(E).
"(E).
Говорят, что отображение f множества Е в пространство Rk принадлежит классу 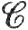 " на E, если каждая его компонента принадлежит классу
" на E, если каждая его компонента принадлежит классу 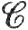 ".
".
Для простоты (и не умаляя общности) мы сформулируем нашу следующую теорему для функций двух переменных.
9.34. Теорема. Если D12f и D21f непрерывны на открытом множестве E⊂R2, то D12f = D21f в Е.
Доказательство. Допустим, что D12f (x)>D21f (x) в какой-нибудь точке х множества Е. Из предположенной непрерывности следует, что тогда существует прямоугольник R, содержащийся в Е, определяемый неравенствами а≤x≤b, α≤y≤β и такой, что (D12f) (х, у)>(D21f) (х, у) при всех (х, у)∈R. Значит,
(74)
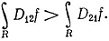
Но
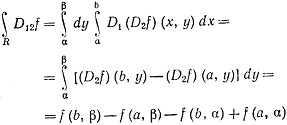
по основной теореме интегрального исчисления, а по теореме 9.29 тот же результат получится и для 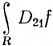 что противоречит неравенству (74).
что противоречит неравенству (74).
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'