
Определители
9.22. Определение. Если (j1, ..., jn) - упорядоченный набор целых чисел, то положим
(54)
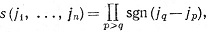
где sgn x = 1, если х>0, sgn x = - 1, если x<0, sgn x = 0, если х = 0. Тогда s(j1, ..., jn) = 1, -1 или 0 и меняет знак, если какие-нибудь два из чисел j меняются местами.
Пусть [А] - матрица линейного оператора А на Rn по отношению к стандартному базису {e1, ..., еn}; на пересечении i-й строки и j-го столбца матрицы [А] стоит число a(i, j). Определителем матрицы [А] называется число
(55)
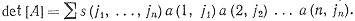
Суммирование в (55) производится по всем упорядоченным наборам целых чисел (j1, ..., jn), таким, что 1≤jr≤n.
Векторы, которые служат столбцами матрицы [А], таковы:
(56)
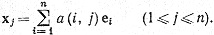
Удобно представлять себе det [A] как функцию столбцов матрицы [A]. Если мы запишем
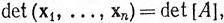
то теперь det - вещественная функция, определенная на множестве всех упорядоченных наборов, состоящих из n векторов пространства Rn.
9.23. Теорема. (а) Если I - тождественный оператор на Rn, то
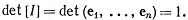
(b) det - линейная функция по каждому из столбцов xj, если остальные фиксированы.
(c) Если [A]1 получается из [A] перестановкой двух столбцов, то det [A]1 = -det [A].
(d) Если матрица [А] имеет два равных столбца, то det [A] = 0.
Доказательство. Если A = I, то a(i, i) = 1, a(i, j) = 0 при i≠j. Значит,
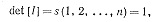
и (а) доказано. Согласно (54), s(j1, ..., jn) = 0, если какие-нибудь два из чисел j равны. Каждое из n! остальных произведений, участвующих в (55), содержит ровно по одному множителю из каждого столбца. Тем самым доказано (b). Утверждение (с) немедленно следует из того, что s(j1, ..., jn) меняет знак, если какие-нибудь два из чисел j равны, a (d) следует из (с).
9.24. Теорема. Пусть [А] и [В] - матрицы операторов, действующих в Rn. Тогда det([В][А]) = det[В] - det[A].
Доказательство. Если х1, ..., хn - столбцы матрицы [A], то положим
(57)
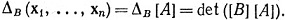
Столбцы матрицы [В][А] - это векторы Bx1, ..., Вхn. Таким образом,
(58)
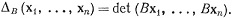
Согласно (58) и теореме 9.23, функция ΔB также обладает свойствами (9.23) (b), (с), (d). Согласно (b) и (56),
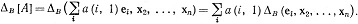
Повторяя эту процедуру с х2, ..., хn, мы получаем
(59)
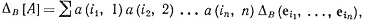
где суммирование распространяется на все упорядоченные наборы (i1, ..., in) с 1≤ir≤n. Согласно (c) и (d),
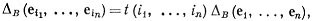
где t = 1, 0 или -1, а так как [В][I] = [В], то из (57) следует, что
(61)
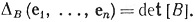
Подставляя (61) и (60) в (59), мы получаем
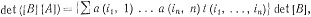
каковы бы ни были матрицы [А] и [В]. Полагая B = I, мы видим, что сумма в фигурных скобках равна det [A]. Теорема доказана.
9.25. Теорема. Линейный оператор А на Rn обратим тогда и только тогда, когда det [A]≠0.
Доказательство. Если А обратим, то, как показывает теорема 9.24,
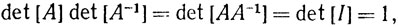
так что det [А]≠0.
Если А не обратим, то столбцы x1, ..., xn матрицы [А] зависимы (теорема 9.5) и, следовательно, имеется столбец, скажем, хk, такой, что
(62)
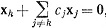
где cj - некоторые числа. Согласно 9.23 (b) и (d), столбец хд можно заменить столбцом xk+cjxj, не меняя определителя, если j≠k. Отсюда следует, что столбец хk, сохраняя значение определителя, можно заменить столбцом, стоящим слева в (62), т. е. столбцом нулей. Но матрица, имеющая 0 одним из своих столбцов, имеет нулевой определитель. Поэтому det[A] = 0.
9.26. Замечание. Пусть {e1, ..., еn} и {u1, ..., un} - базисы в Rn. Каждому линейному оператору в Rn отвечают матрицы [А] и [А]U с элементами аij и αij в соответствии с равенствами
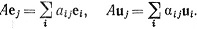
Если 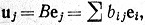 то вектор Auj равен вектору
то вектор Auj равен вектору
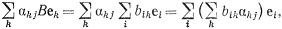
а также вектору
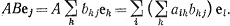
Таким образом, 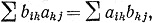 или
или
(63)
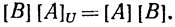
Поскольку оператор В обратим, то det[B] = ≠0. Комбинируя (63) с теоремой 9.24, получаем
(64)
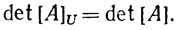
Поэтому определитель матрицы линейного оператора не зависит от базиса, который был использован для построения матрицы. Таким образом, имеет смысл говорить об определителе линейного оператора, не имея при этом в виду никакого базиса.
9.27. Якобианы. Пусть f отображает открытое множество Е⊂Rn в пространство Rn. Если f дифференцируемо в точке х∈Е, то определитель линейного оператора f'(х) называется якобианом отображения f в точке х. Якобиан отображения f в точке х обозначается символом Jf(х), так что
(65)
Jf(x) = det f'(x).
Мы будем использовать для Jf(x) также обозначение
(66)
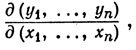
если {у1, ..., уn) = f (х1, ..., хn).
Используя понятие якобиана, основное условие теоремы об обратной функции можно записать так: Jf(а)≠0 (ср. с теоремой 9.25). Если теорему о неявной функции сформулировать в терминах функций (35), то условие этой теоремы сводится к неравенству
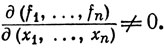
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'