Теорема о разложении

Пусть f - отображение открытого множества E⊂Rⁿ в пространство Rⁿ, и пусть существует такое целое j, что e_i*f(х)=е_i*х при всех i≠j, х∈Е. Таким образом, х и f(x) имеют равные i-e координаты при i≠j, т. е. отображение f может изменять только j-ю координату. Мы будем называть такие отображения простыми.

9.21. Теорема. Пусть f есть 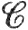' - отображение открытого множества E⊂R_n в пространство R_n, 0∈E, f(0) = 0, а f'(0) - обратимое преобразование. Тогда существует такая окрестность нуля в Rⁿ, в которой имеет место представление

Здесь каждое g_k - простое 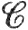' - отображение некоторой окрестности точки 0, g_k (0) = 0, а каждое B_k - линейное отображение на Rⁿ, причем либо тождественное, либо меняющее местами какую-нибудь одну пару координат.

Доказательство. Положим f = f₁, и пусть 1≤m≤n. Приведем следующее индуктивное предположение (очевидно, справедливое при m = 1):f_m отображает окрестность точки 0 пространства Rⁿ в пространствр Rⁿ, f_m - отображение класса 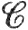', преобразование A_m = f'_m(0) обратимо и

(48)

Положим α_ij = e_i*A_me_j. Из (48) следует, что α_ij = 0, если i<m и j≥m. Если бы, кроме того, при всех j≥m выполнялось равенство α_mj = 0, то из представления 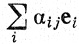следовало бы, что n+m-1 независимых векторов A_me_m, ..., А_nе_n принадлежат оболочке n-m векторов e_m+1, ..., е_n, вопреки теореме 9.2.

Таким образом, существует такое j, что m≤j≤n и α_mj≠0.

Определим операторы P_m, B_m∈L(Rⁿ) равенствами: P_me_i = e_i, если i≠m, P_me_m = 0; B_me_m = e_j, B_me_j = е_m, B_mе_i = e_i, для всех прочих i. Положим

(49)

Тогда g_m, очевидно, простое отображение. Поскольку (f_mB_m)'(0) = A_mB_m, то

(50)

Если g_m(0)h=0, то, как показывает (50), P_mh = 0, так что h = λ*e_m. Но, кроме того, e_m*A_mB_mh = 0, т. е. λα_mj = 0 по определению В_m. Поскольку α_mj≠0, мы видим, что λ = 0, значит, h = 0.

Тем самым доказано, что g_m(0) - взаимно однозначное отображение. Стало быть, оно обратимо, и из теоремы об обратном отображении следует, что g_m взаимно однозначно в некоторой окрестности U_m точки 0 и что g_m (U_m) = V_m - открытое множество в Rⁿ. Положим

(51)

Если y∈V_m, y = g_m(x), x∈U_m, то, как показывает (49),

(52)

Теперь из (48) и определения В_m следует, что

если i<m; из (52), кроме того, следует, что

Следовательно, f_m+1 удовлетворяет предположению индукции с m+1 вместо m, и построение можно продолжить. Переписывая (51) в виде

(53)

при m = 1, ..., n и замечая, что f_n+1 - тождественное отображение, мы получаем

что и составляет нужное заключение.