Теорема о ранге [1976 Рудин У. - Основы математического анализа]

НОВОСТИ БИБЛИОТЕКА ЭНЦИКЛОПЕДИЯ БИОГРАФИИ КАРТА САЙТА ССЫЛКИ О ПРОЕКТЕ

Теорема о ранге

Назовем рангом линейного преобразования размерность его множества значений. Следующая теорема служит подготовительной к теореме 9.20.

9.19. Теорема. Пусть р, q, r - неотрицательные целые числа, X и Y - векторные пространства, dim X = r+p, dim Y =r+q, А - линейное преобразование пространства X в пространство Y ранга r. Тогда существуют векторные пространства Х₁, Х₂, содержащиеся в X, и пространства Y₁, Y₂, содержащиеся в Y, такие, что

(a) каждый х∈Х единственным образом представим в виде

x = x₁ + x₂, где x₁&38712;X₁, х₂∈Х₂;

(b) каждый у∉Y единственным образом представим в виде

у = y₁ + у₂, где y₁∈Y₁, y₂∈Y₂;

(c) Aх₂ = 0 при каждом _х₂&38712;_Х₂;

(d) сужение преобразования А на Х₁ - взаимно однозначное отображение пространства X₁ на пространство Y₁;

(e) dim X₁ = dim Y₁ = r.

Доказательство. По теореме 9.3 (с) пространство Y имеет базис {v₁, ...,v_r+q}, такой, что {v₁, ..., v_r} - базис множества значений У₁ преобразования А. Пусть У₂ - оболочка множества {v_r+1, ..., v_r+q}. (Заметим, что если q = 0, то Y₂ состоит из одного лишь нулевого вектора. Некоторые утверждения, высказанные в ходе этого доказательства и в теореме 9.20, должны быть истолкованы аналогично, если одно или более из чисел р, q, r равны нулю. Мы предоставляем читателю подправить эти утверждения и истолковать их.)

Выберем векторы u₁, ..., u_r∈X, такие, что Au_j = v_j (1≤j≤r). Тогда {u₁, ..., u_r} - независимое множество; натянем на него пространство X₁. Пусть Х₂ - множество всех х∈Х, таких, что Aх = 0.

Ясно, что утверждения от (b) до (е) выполняются. Если х∈Х, то 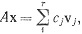где c₁, ..., c_r - некоторые числа. Положим 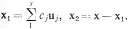Тогда x₁∈X₁, Ax₁ = Ax; значит, Aх₂ = 0, или х₂∈Х₂. Согласно (с) и (d), Х₁ и Х₂ имеют только один общий вектор - нулевой. Поэтому представление х = x₁ + x₂ единственно, и (а) доказано. Следующая теорема еще раз иллюстрирует общий принцип, состоящий в том, что непрерывно дифференцируемое отображение F вблизи точки х ведет себя примерно так же, как линейное преобразование F'(х).

9.20. Теорема. Пусть X = R^r+p, Y = R^r+q, F есть 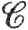' - отображение открытого множества Е?№8834жX в пространство Y и F'(х) - линейное преобразование ранга r при любом х∈Е.

Зафиксируем точку а∈E, положим A = F'(a), выберем Х₁, Х₂, У₁ и У₂, как в теореме 9.19, и определим F₁ и F₂ равенством

(39)

F(x) = F₁(x)+F₂(x) (x∈E),

где F₁(x)∈Y₁, F₂(x)∈Y₂.

Тогда существует открытое множество U в пространстве X, такое, что а∈U, U⊂Е и

(a) F₁(U) - открытое множество в Y₁;

(b) для любого y∈F₁(U) существует ровно один y₂∈Y₂, такой, что

y₁+y₂∈F(U).

Геометрический смысл утверждения (b) таков: F(U) - это "r-мерная поверхность" в Y, причем "над" каждой точкой множества F₁(U) лежит ровно одна точка этой поверхности. Мы советуем читателю набросать чертеж для случаев, когда числа p, q, r принимают одно из значений 0, 1, 2.

Доказательство. Пусть Т - сужение отображения А на X₁. Согласно 9.19 (d), T - линейное взаимно однозначное преобразование пространства X₁ на Y₁, а обратное преобразование Т^-1 отображает Y₁ на X₁. Пусть Р - линейный оператор на X, определенный так: Рх = х₂, если x = х₁+x₂, x₁∈X₁, х₂∈Х₂ (такого рода оператор называют проектором), и пусть

(40)

f(х) = T^-1F'(х)+Рx (х∈E).

Согласно правилу дифференцирования сложной функции,

(41)

f'(a) = T^-1F'₁(a)+P.

При i = 1, 2 множество значений отображения F_i содержится в Y_i. Поскольку Y_i - замкнутое подпространство пространства Y, то из (18) ясно что F'_i(a)h∈Y_i при всех h∈X. Согласно (39), A = F'₁(a) + F'₂(a); а так как множество значений отображения А совпадает с Y₁, то, по теореме 9.19 (b), A = F'₁(a), и 9.19 (с) показывает, что Ah = Ah₁, если h = h₁ + h₂, h₁∈X₁, h₂∈Х₂. Таким образом,

f'(a)h = T^-1Ah + Ph = Т^-1Аh₁ + h₂ = h₁ + h₂ = h.

Это значит, что f'(а) - тождественное отображение на X. Поэтому из теоремы об обратной функции следует, что существуют открытые множества U и V в X, такие, что а∈U, U⊂Е и f - взаимно однозначное отображение множества U на V. Более того (заменяя, если потребуется, V и V надлежащими множествами), можно добиться, чтобы V было выпуклым. Пусть g - отображение множества V на U, обратное к f. Положим

(42)

Φ(z) = F(g(z)) (z∈V).

Из того, что АР = 0, следует, что Af = AT^-1F₁ = F₁, так что

F₁(g(z)) = Af(g(z)) = Az = Az₁.

Таким образом,

(43)

Φ(z) = Az₁+φ(z) (z∈V),

где φ(z)∈Y₂, z = z₁+z₂, z₁∈X₁, z₂∈X₂

Согласно (42) и (43), F₁(U) - это множество всех точек Az₁, где z∈V. Поскольку V открыто, а Y₁ - множество значений отображения А, то утверждение (а) теоремы доказано.

Чтобы доказать (b), достаточно проверить, что Φ(z) зависит только от z₁.

Зафиксируем z∈V. Согласно (42) и (43),

(44)

Φ'(z) = F'(g(z))g'(z)=A+φ'(z).

Ввиду того что g'(z) - обратимый линейный оператор на X, a F'(g (z)) - отображение ранга r, множество значений R отображения Φ'(z) - векторное пространство размерности r. Пусть Q - проектор пространства У на пространство Y₁. Поскольку множество значений отображения φ'(z) содержится в Y₂, то (44) показывает, что A = QΦ'(z). Таким образом, Q отображает пространство R на Y₁, а так как размерность обоих этих пространств равна r, то Q взаимно однозначно на R. Таким образом,

(45)

из Ah = 0 следует, что Φ'(z) h = 0.

Если теперь z∈V, z+h₂∈V, h₂∈'X₂, то положим

(46)

Λ(t) = Φ(z + th₂) (0≤t≤1).

Поскольку V выпукло, это определение имеет смысл, а так как Ah₂ = 0, то из (45) и (46) следует, что

(47)

Λ'(t) = Φ'(z + th₂)h₂ = 0 (0≤t≤1).

Таким образом, Λ(1) = Λ(0), так что Φ(z + h₂) = Φ(z) и (b) установлено.

ПОИСК:

© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'