Теорема о неявной функции

Если x = (x₁, ..., x_n)∈Rⁿ и y = (y₁, ..., y_m)∈R^m, то через (х, у) мы будем обозначать точку (или вектор)

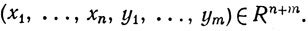
В этом разделе первый элемент в (х, у) или в подобном символе всегда будет обозначать вектор пространства Rⁿ, а второй - вектор пространства R^m.

Пусть A∈L(R^n+m, Rⁿ), и пусть

(32)

Заметим, что по теореме 9.5 отображение h⊂A(h, 0) есть линейное взаимно однозначное отображение Rⁿна себя. Далее, при всяком k∈R^m и b∈Rⁿ уравнение А (х, k) = b имеет единственное решение. Действительно, существует такое х, что А (х, 0) = b-A(0, k), т. е. A(х, k) = b, а если А(х₁, k) = А(х₂, k), то A(х₁-х₂, 0) = 0 и, в силу (32), x₁ = x₂.

В частности, если А удовлетворяет условию (32), то уравнение

(33)

имеет при каждом у∈R^m одно и только одно решение х∈Rⁿ.

Теорема о неявной функции утверждает, что подобное заключение справедливо и в отношении некоторых (не обязательно линейных) непрерывно дифференцируемых отображений. Прежде чем сформулировать ее, заметим, что если [A] - матрица (из n строк и n+m столбцов) отображения A по отношению к стандартным базисам, то (32) означает в точности, что векторы, стоящие в первых n столбцах матрицы [A], линейно независимы. Пользуясь этим критерием, можно проверять, выполняется ли (32).

9.18. Теорема. Пусть f есть 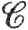' - отображение открытого множества Е⊂R^n+m в пространство Rⁿ. Допустим, что (а, b)∈Е, f(a, b) = 0, A = f'(а, b) и А удовлетворяет условию (32). Тогда существуют окрестность W точки b (W⊂R^m) и единственная функция g∈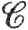'(W) со значениями в Rⁿ, такие, что g(b) = а и

Функция g определена неявно равенством (34), отсюда и название теоремы. Ее можно сформулировать в терминах, относящихся к системе n уравнений с n+m неизвестными:

Наше предположение об А теперь означает, чго квадратная матрица из n строк и n столбцов, такая, что на пересечении ее i-й строки и j-го столбца стоит 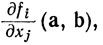имеет независимые столбцы. Если это выполняется и если х = а, у = b удовлетворяют уравнению (35), то (35) можно разрешить относительно х₁, ... , х_n при каждом у, достаточно близком к b.

Доказательство. Пусть F - отображение, ставящее в соответствие точке (х, у)∈Е точку (z, w)∈R^n+m, определенную равенством

(36)

Тогда F∈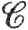'(E) поскольку f(a, b) = 0, то

где r - остаток, участвующий в определении f'. Из того что

следует, что F'(a, b) - линейный оператор на Rn+m, который вектору (h, k) ставит в соответствие вектор (A (h, k), k). Если при таком отображении образ какого-нибудь вектора равен нулю, то A (h, k) = 0 и k = 0, а потому A (h, 0) = 0 и из (32) следует, что h = 0. Это значит, что оператор F'(а, b) взаимно однозначен и, следовательно, обратим (теорема 9.5).

Поэтому к F применима теорема об обратной функции: существуют открытые множества U и V в R^n+m, содержащие (а, b) и (0, b) и такие, что F взаимно однозначно отображает U на V; согласно (36), отображение, обратное к F, имеет вид

(37)

где φ∈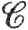'(V). Иными словами,

(38)

Если мы теперь обозначим через W такую окрестность точки b, что (0, w)∈V при w∈W, и положим g(y) = φ(0, y) при у∈W, то при z = 0 в (38) мы получим (34).

Ясно, что g (b) = а, так как φ(0, b) = а. Единственность функции g следует из того, что отображение F взаимно однозначно: если (х, у)∈U, (х^*, у)∈U, a f(x, y) = f(x^*, у), то F(x, y) = F(x^*, у), а потому х^* = х.