Теорема об обратной функции

Эта теорема утверждает, грубо говоря, что непрерывно дифференцируемое отображение f обратимо в окрестности любой точки х, в которой обратимо линейное преобразование f'(х).

9.17. Теорема. Пусть f есть 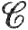' - отображение открытого множества Е⊂Rⁿ в пространство Rⁿ, пусть отображение f'(a) обратимо при некотором а∈E, и пусть b = f(a). Тогда

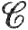то g∈'(V).

Записывая равенство у = f (x) с помощью компонент, мы приходим к следующей интерпретации заключения теоремы: равенства

определяют взаимно однозначное соответствие между достаточно малыми окрестностями точек а и b; при этом.x₁, ..., х_n являются непрерывно дифференцируемыми функциями от у₁, ..., у_n.

Доказательство. Пусть f'(а) = А. Выберем X так, чтобы 4λ ||A^-1|| = 1. Ввиду того что f∈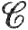'(E), существует такой открытый шар U с центром в точке а, что

(22)

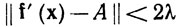
(x∈U).

Допустим, что х∈U и х+h∈U. Положим

Вследствие выпуклости множества U, x+th∈U при 0≤t≤1, и из (22) следует, что

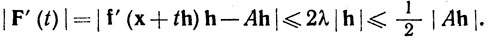
Последнее неравенство выполняется потому, что

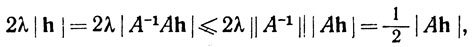
в силу выбора числа X. Из теоремы 5.20 следует теперь, что

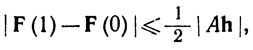
или

(23)

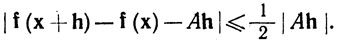
Отсюда следует, что

(24)

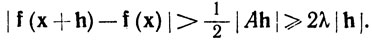
Подчеркнем, что неравенства (23) и (24) выполняются, если только x∈U и x+h∈U. В частности, из (24) следует, что отображение f взаимно однозначно на U.

Зафиксируем x₀∈U и рассмотрим открытый шар S с центром в точке х₀ радиуса r>0, замыкание которого лежит в U. Мы докажем, что f(S) содержит открытый шар с центром в точке f (х₀) радиуса λr.

Чтобы сделать это, зафиксируем такой вектор у, что |у-f(х₀)|<λr, и положим

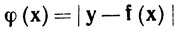
(x∈).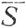

Если то, как показывает (24),

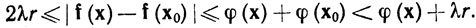
Таким образом,

(25)

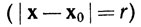
Ввиду того что φ - непрерывная функция, a 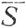- компактное множество, существует x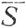^*∈, такой, что φ(х^*)≤φ(х) при всех х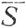^*∈. Согласно (25), x^*∈S.

Положим w = y-f(x^*). Поскольку А обратим, существует вектор h∈Rⁿ, такой, что Ah = w. Выберем число t∈(0, 1), столь малое, что x^*+th∈S. Тогда

(26)

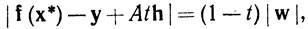
и, как показывает (23),

(27)

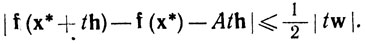
Поскольку φ(х^*+th) - норма суммы векторов, фигурирующих в левых частях равенства (26) и неравенства (27), и так как |w| = φ(х^*), то

(28)

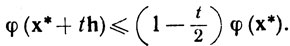
Таким образом, φ(х^*) = 0, т. е. f(x^*)=у.^*

^* (Эту часть доказательства можно еще немного сократить. Действительно, функция 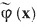=|у-f(x)|² достигает минимума в точке х^*, принадлежащей S. Поэтому частные производные функции 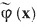в этой точке обращаются в нуль. Отсюда следует, что В(y-f(x^*)) = 0, где B∈L(Rⁿ, Rⁿ), [В] - матрица, транспонированная к [f'(x^*)] и потому обратимая. Значит, y = f(x^*).- Прим. перев.)

Тем самым доказано, что каждая точка множества f(U) имеет окрестность, содержащуюся в f(U). Поэтому f(U) - открытое подмножество пространства Rⁿ. Полагая V = f(U), мы видим, что утверждение (а) теоремы доказано.

Чтобы доказать (b), выберем y∈V, y+k∈V и положим x = g(y),

Согласно теореме 9.8 (а), неравенству (22) и нашему выбору числа λ, оператор f'(х) имеет обратный, который мы обозначим через В. Применяя В к равенству

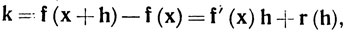
где 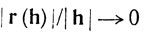при h→0, мы получим Bk = h + Br(h), или

(29)

Согласно (24), 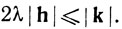Таким образом, h→0 при k→0 (что одновременно доказывает непрерывность отображения g в точке у) и

(30)

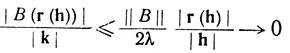
при k→0.

Сравнение (30) и (29) показывает, что g дифференцируемо в точке у и что g'(у) = В. Иными словами,

(31)

Кроме того, g - непрерывное отображение множества V на U, f' - непрерывное отображение множества V в множество Ω всех обратимых элементов множества L(Rⁿ), а переход к обратному - непрерывное отображение множества Ω на множество Ω [по теореме 9.8 (b)]. Используя эти факты и равенство (31), мы получаем, что g∈'(V).

Теорема доказана.

Следующее утверждение вытекает непосредственно из теоремы [часть (а)]:

Следствие. Если f есть ' - отображение открытого множества Е⊂Rⁿ в пространство Rⁿ и если оператор f'(х) обратим при любом х∈Е, то f(W) - открытое подмножество пространства Rⁿ, каково бы ни было открытое множество W⊂E.

Иными словами, f - открытое отображение множества Е в пространство Rn.

Предположения, сделанные в этом следствии, обеспечивают для каждой точки х∈Е существование такой окрестности, на которой отображение f взаимно однозначно. Можно сказать, что f локально взаимно однозначно. Однако f не обязано при этом быть взаимно однозначным на всем множестве Е. Пример приведен в упражнении 12.