Дифференцирование

9.10. Определение. Пусть Е - открытое множество в Rⁿ, f - отображение множества Е в пространство R^m и х∈E.

Если существует линейное преобразование А пространства Rⁿ в пространство R^m, такое, что

(5)

то говорят, что f дифференцируемо в точке х, и пишут

(6)

Если отображение f дифференцируемо в каждой точке х∈Е, то говорят, что fдифференцируемо на множестве Е.

Следующие комментарии приводятся для разъяснения и мотивировки этого определения.

(а) В (5), конечно, имеется в виду, что h∈Rⁿ, а потому если норма |h| достаточно мала, то х+h∈E, так как E - открытое множество. Таким образом, f(x+h) имеет смысл, f (x+h)∈R^m, и так как A∈L(Rⁿ, R^m), то Ah∈R^m. Таким образом,

Норма, фигурирующая в числителе дроби (5),- это норма пространства R^m, а в знаменателе - Rⁿ-норма вектора h.

(b) В случае n = 1 новое определение производной сводится к прежнему (см. определение 5.1 и п. 5.16). Производная f'(х) определялась как вектор y∈R^m (если только он существует), для которого

(7)

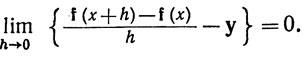
Но всякому вектору у∈R^m можно (взаимно однозначно) сопоставить линейное преобразование Т_у пространства R¹ в R^m по формуле T_yh = hy. Заметим, что каждое T∈L(R¹, R^m) имеет вид Т = Т_y при некотором у (нужно просто взять у = T1). При этом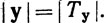

(c) Пусть f и Е - те же, что в определении 9.10, и пусть f дифференцируемо на Е. При каждом фиксированном х∈Е f(х) = A есть линейное преобразование пространства Rⁿ в R^m, т. е. функция, сопоставляющая каждому вектору h∈Rⁿ вектор ^f'(х) ^h = Ah∈R^m. С другой стороны, поскольку отображение f дифференцируемо в каждой точке множества Е, то каждой точке этого множества соответствует оператор f'(х) = А. Тем самым дифференцируемое отображение f индуцирует отображение (функцию) f' на Е со значениями в L(Rⁿ, R^m).

(d) Соотношение (5) можно переписать в виде

(8)

где остаток r(h) мал в том смысле, что

(9)

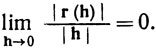
Можно истолковать (8) так: при фиксированном х и малом h разность

приближенно равна f'(x) h, т. е. равна значению линейной функции в точке h.

Достаточно взглянуть на равенство (8), чтобы убедиться в непрерывности отображения f в любой точке, в которой оно дифференцируемо.

(e) Производную, определенную в (5) или в (8), часто называют полной производной отображения f в точке х, или дифференциалом отображения f в точке х.

Теперь мы решим вопрос о единственности, который, возможно, уже возник у читателя.

9.11. Теорема. Пусть Е и f - те же, что в определении 9.10, х∈E и (5) выполняется с A = A₁ и с А = А₂, где A₁∈L(Rⁿ, R^m) (i = 1, 2). Тогда А₁ = А₂.

Доказательство. Если В = А₁ - А₂, то неравенство

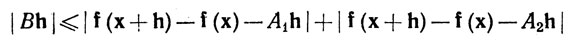
показывает, что 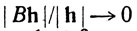при h→0. Отсюда следует, что при фиксированном h≠0

(10)

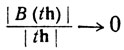
при t→0.

Ввиду того что В линейно, левая часть в (10) не зависит от t. Поэтому Bh = 0 при всех h∈Rⁿ. Теорема доказана.

Правило дифференцирования сложной функции (см. теорему 5.5) легко распространяется на данную ситуацию. И формулировка, и доказательство совершенно такие же, как в одномерном случае.

9.12. Теорема. Пусть Е - открытое множество в пространстве Rⁿ, f - отображение множества Е в пространство R^m, дифференцируемое в точке х₀∈Е, g - отображение некоторого открытого множества, содержащего ^f(E), в пространство R^k, причем g дифференцируемо в точке f (х₀). Тогда отображение F множества Е в пространство R^h, определенное равенством

дифференцируемо в точке х₀, и

(11)

В правой части равенства (11) стоит произведение двух линейных преобразований, определенное в разделе 9.6.

Доказательство. Пусть y₀ = f(x₀), A = f'(х₀), B = g'(y₀), и пусть

Мы должны доказать, что F'(х₀) = ВА, т. е. что

(12)

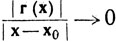
при х→х₀.

Из определений отображения F и остатка r имеем

так что

(13)

Если ε>0, то из определения преобразований А и В следует, что существуют η>0 и δ>0, такие, что

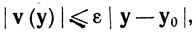
есл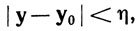и и

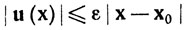
при 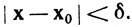Значит,

(14)

и

(15)

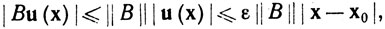
если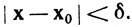

Теперь (12) следует из (13), (14) и (15).

9.13. Частные производные. Пусть f отображает открытое множество Е⊂Rⁿ в пространство R^m и имеет компоненты f₁,..., f_m, определенные в теореме 4.10. Пусть (e₁, ..., e_n} - стандартный базис пространства Rⁿ. Определим на множестве Е функции D_jf_i равенствами

(16)

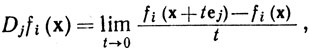
если, конечно, этот предел существует. Записывая f_i(x) в виде f_i{x₁, ..., x_n), мы видим, что D_jf_i есть производная функции f_i по x_j при фиксированном значении остальных переменных. Поэтому часто используется обозначение

(17)

вместо D_jf_i.

Если отображение f дифференцируемо в точке х, то определение производной f'(x) показывает, что

(18)

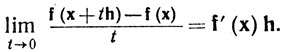
Переходя к координатам векторов, стоящих в (18), с h = e_j, мы видим, что если f дифференцируемо в точке х, то все частные производные (D_jf_i) (x) существуют.

Обратное, вообще говоря, неверно даже в том случае, когда частные производные существуют во всех точках множества Е (упражнение 9); если, однако, частные производные к тому же непрерывны, то обратное верно (см. теорему 9.16).

Отметим, что f'(х)е_j - это j-й столбец матрицы [f(x)]. Таким образом, (D_jf_i) (x) находится в i-й строке и j-м столбце матрицы [f'(х)].

9.14. Пример. Пусть f - дифференцируемое отображение интервала (a, b)⊂R¹ в открытое множество E⊂Rⁿ, пусть g - дифференцируемая вещественная функция, определенная в Е (т. е. g - дифференцируемое отображение множества Е в пространство R¹). Положим h(t) = g(f(t)) при a<t<b. Согласно правилу дифференцирования сложной функции,

Ясно, что h'(t) - линейный оператор на R¹, так как f'(t)∈L(R¹, Rⁿ) и g'(f(t))∈L(Rⁿ, R¹). Если рассматривать h'(t) как вещественное число, то оператор, о котором идет речь,- это оператор умножения на h'(t); ср. с 9.10 (b).

По отношению к стандартному базису пространства Rⁿ [f'(t)] - это матрица из n строк и 1 столбца ("одностолбцовая матрица"), в i-й строке которой стоит f'_i(t), где f₁, ..., f_n - компоненты отображения f, и при каждом х∈Е [g'(x)] - матрица из 1 строки и n столбцов ("однострочная матрица"), в j-м столбце которой стоит (D_jg)(x). Значит, [h'(t)] - матрица из одной строки и одного столбца, единственным элементом которой служит вещественное число

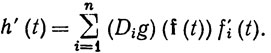
Написанное равенство - часто встречающийся случай правила дифференцирования сложной функции.

9.15. Определение. Дифференцируемое отображение f открытого множества Е⊂Rⁿ в пространство R^m называется непрерывно дифференцируемым на Е, если f' - непрерывное отображение множества Е в пространство L(Rⁿ, R^m).

Говоря более отчетливо, в этом определении требуется, чтобы для любого х∈E и любого ε>0 существовало число δ>0, такое, что 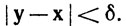если у∈E и |y-x|<δ

Если это выполняется, то мы будем говорить, что f является 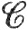' - отображением на Е или что f∈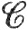'(E).

9.16. Теорема. Пусть f отображает открытое множество Е⊂Rⁿ в пространство R^m. Тогда f∈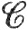'(E) в том и только в том случае, когда частные производные D_jf_i существуют и непрерывны на Е при 1≤i≤m, 1≤j≤n.

Доказательство. Если f∈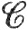'(E), то неравенство

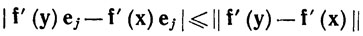
в сочетании с (16) и (18) показывает, что каждая частная производная D_jf_i - непрерывная функция на Е.

Для доказательства обратного достаточно рассмотреть случай m = 1 (почему?). Зафиксируем х∈Е и ε>0. Ввиду того что множество Е открыто, существует открытый шар 5 с центром в точке х и радиусом r, целиком принадлежащий Е. Из непрерывности функций D_jf следует, что r можно выбрать столь малым, чтобы иметь

(19)

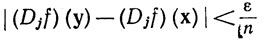
(y∈S, 1≤j≤n.)

Пусть h = ∑h_je_j, 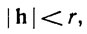пусть v₀ = 0 и v_k = h₁e₁ + ... + h_ke_k при 1≤k≤n. Тогда

(20)

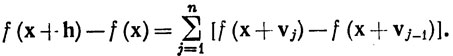
Ввиду того что |v_k|<r при 1≤k≤n, а множество S выпукло, отрезки с концами x+v_j-1 и x+v_j лежат в S. Поскольку v_j = v_j-1+h_je_j, то по теореме 5.10 о среднем значении j-е слагаемое в (20) равно

(21)

при некотором θ_j∈(0,1), и потому оно в силу (19) отличается от h_j(D_jf)(x) менее, чем на |h_j|ε/n. Согласно (20), отсюда следует, что

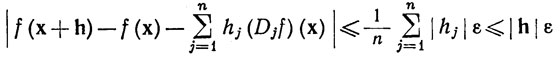
при всех h, таких, что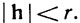

Это означает, что функция f дифференцируема в точке х и что f'(х) - линейная функция, которая ставит в соответствие число ∑ h_j (D_jf) (х) вектору h = ∑ h_je_j. Матрица [f'(х)] состоит из строки (D₁f) (х), ..., (D_nf) (x), а так как функций D₁f, ...,D_nf непрерывны на Е, то, как показывает заключительное замечание п. 9.9, f∈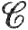'(E).