
Глава 9. Функции нескольких переменных
Линейные преобразования
Эту главу мы начнем с рассмотрения множеств векторов в евклидовом пространстве Rn. Излагаемые здесь алгебраические факты без изменений переносятся на конечномерные векторные пространства над любым полем скаляров. Однако для наших целей мы вполне можем оставаться в привычных рамках евклидовых пространств
9.1.Определения. (а) Множество X⊂Rn называется векторным пространством, если х + у∈Х и сх∈Х, каковы бы ни были х∈Х, у∈Х и число с.
(b) Если x1, ..., xkẄRn, a c1, ..., ck - числа, то вектор c1x1 + ... + ckxk называется линейной комбинацией векторов x1, ..., xk. Если S⊂Rn и если Е - множество всех линейных комбинаций элементов S, то мы будем говорить, что Е натянуто на S или что Е - оболочка S.
Заметим, что каждая оболочка есть векторное пространство.
(c) Множество, состоящее из векторов x1, ..., xk (для такого множества мы будем использовать обозначение {x1, ..., xk}), называется независимым, если из соотношения c1x1 + ... + ckxk = 0 следует, что c1 = ... = сk = 0. В противном случае это множество называется зависимым.
Отметим, что независимое множество не может содержать нулевого вектора.
(d) Если векторное пространство X содержит независимое множество, состоящее из r векторов, но не содержит никакого независимого множества из r + 1 векторов, то говорят, что X имеет размерность r и пишут dim X = r.
Множество, состоящее из одного элемента 0,- векторное пространство; размерность его равна нулю.
(e) Независимое подмножество пространства X, оболочка которого равна X, называется базисом пространства X.
Заметим, что если B = {x1, ..., хr} - базис пространства X, то каждый элемент х∈X допускает единственное представление вида х = ∑cjxj. Такое представление существует, так как Х натянуто на В, и единственно, так как множество В независимо. Числа с1, ... , сr называются координатами вектора х по отношению к базису В.
Наиболее известным примером базиса служит множество {e1, ... , еn}, где еj - вектор пространства Rn, j-я координата которого равна 1, а прочие координаты равны нулю. Если x∈Rn, х = (х1, ... , хn), то х = ∑xjej. Мы будем называть множество {е1, ..., еn} стандартным базисом пространства Rn.
9.2. Теорема. Пусть r - положительное целое число. Если векторное пространство X натянуто на множество, состоящее из r векторов, то dim X≤r.
Доказательство. Если это неверно, то существует векторное пространство X, содержащее независимое множество Q = {y1, ... , yr+1} и натянутое на множество S0, состоящее из r векторов.
Пусть 0≤i<r, и допустим, что построено множество Si, оболочкой которого служит пространство X и которое состоит из векторов уj с 1≤j≤i и из некоторого набора r - i векторов множества S0, скажем х1, ..., xr - i. (Иными словами, Si получается из множества S0 заменой i из его элементов элементами множества Q без изменения оболочки.) Поскольку X натянуто на Si, то yi+1 принадлежит оболочке множества Si, значит, существуют числа а1, ..., ai+1, b1, ..., br-i, где ai+1 = 1, такие, что
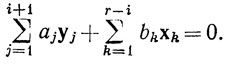
Если бы все bk были равны нулю, то, в силу независимости множества Q, и все аj были бы нулями. Но ai+1= 1. Следовательно, некоторый вектор xk∈Si есть линейная комбинация других элементов множества Ti = Si∪{yi+1}. Удалим этот вектор хk из Ti и обозначим оставшееся множество через Si+1. Тогда оболочка множеств Si+1 и Ti равна X, так что Si+1 обладает теми же свойствами, что и Si (только i нужно заменить на i+1).
Начиная с S0, мы построим таким образом множества S1, ..., Sr. Последнее из них состоит из у1, ..., уr, и наше построение показывает, что его оболочка равна X. Но множество Q независимо, значит, уr+1 не принадлежит оболочке множества Sr. Это противоречие доказывает теорему.
Следствие. dim Rn = n.
Доказательство. Пространство Rn натянуто на множество {е1, ...,еn}. Поэтому, как показывает теорема,
dim Rn = ≤ n.
Но множество {e1, ..., еn} - независимое, и потому dim Rn ≥ n.
9.3. Теорема. Пусть X - векторное пространство и dim X = n.
(a) Пространство X натянуто на множество Е, состоящее из n векторов, в том и только в том случае, когда множество Е независимо.
(b) X имеет базис, и каждый базис состоит из n векторов.
(c) Если 1≤r≤n и {у1, ... , уr} - независимое множество в X, то X имеет базис, в состав которого входят все векторы y1, ..., yr.
Доказательство. Пусть Е = {x1, ..., хn}. Множество {x1, ..., хn, у) зависимо при любом у∈Х, так как dim X = n. Если Е независимо, то у принадлежит оболочке множества Е; значит, X натянуто на Е. Обратно, если множество Е зависимо, то один из его элементов можно удалить, не меняя оболочки. Значит, X не может быть оболочкой множества Е по теореме 9.2. Тем самым (а) доказано.
Пространство X содержит независимое множество, состоящее из n векторов, так как dim X = n, а согласно (а), каждое такое множество образует базис пространства X; теперь (b) вытекает из 9.1 (d) и 9.2.
Чтобы доказать (с), допустим, что {х1, ..., xn} - базис пространства X. Пространство X натянуто на множество
S = {y1, ..., yr, х1, ..., хn},
причем множество S зависимо, так как оно содержит больше, чем n векторов. Рассуждение, использованное при доказательстве теоремы 9.2, показывает, что один из векторов xi равен линейной комбинации остальных элементов множества S. Удалив этот вектор xi из S, мы получим множество, оболочка которого все еще совпадает с X. Повторяя этот процесс r раз, мы получим базис пространства X, содержащий векторы {y1, ..., yr} согласно (а).
9.4. Определение. Отображение А векторного пространства X в векторное пространство Y называется линейным преобразованием, если
A(х1 + х2) = Ax1 + Ax2, A(cx) = cAx,
каковы бы ни были х, х1, х2∈Х и число с. Заметим, что часто пишут Ах вместо А(х), если A - линейное преобразование.
Заметим еще, что если A - линейное преобразование, то A0 = 0. Линейные преобразования пространства X в X часто называют линейными операторами на X*. Если A - линейный оператор на X, который (i) взаимно однозначен; (ii) отображает пространство X на X, называют обратимым. В этом случае на X можно определить оператор А-1, положив A-1(Aх) = х при всех x∈Х. Очевидно, что в этом случае A(A-1х) = х при всех х∈Х и А-1 - линейный оператор.
* (Столь же часто этот термин употребляют применительно к линейным преобразованиям пространства X в отличное от него пространство У.- Прим. перев.)
Важное свойство линейных операторов на конечномерных векторных пространствах состоит в том, что каждое из условий (i) и (ii) влечет за собой другое.
9.5. Теорема. Линейный оператор А на конечномерном векторном пространстве X взаимно однозначен в том и только в том случае, когда множество его значений совпадает со всем X.
Доказательство. Пусть {x1, ...,xn} - базис пространства X. Из свойств линейности оператора А следует, что его множество значений R(A) натянуто на множество Q = {Ax1, ..., Ахn). Из теоремы 9.3. (а) мы заключаем, что R(A) = X тогда и только тогда, когда Q - независимое множество. Мы должны показать, что это происходит тогда и только тогда, когда оператор А взаимно однозначен.
Допустим, что оператор А взаимно однозначен и что ∑ciAixi = 0. Тогда A( ∑cixi) = 0, значит, ∑cixi = 0, значит, с1 = ... = сn = 0, и мы заключаем, что множество Q независимо.
Пусть, обратно, Q независимо и A(∑cixi) = 0. Тогда ∑ciAxi = 0, значит, c1 = ... = сn = 0, и мы заключаем: Ах = 0 только тогда, когда х = 0. Если теперь Ах = Ау, то А (х - у) = Ах - Ау = 0, так что х - у = 0, и потому А взаимно однозначен.
9.6. Определение.(а). Пусть L(X, Y) - множество всех линейных отображений векторного пространства X в векторное пространство Y. Вместо L (X, X) мы будем писать просто L (X). Если А1, A2∈L(X, Y) и если с1, с2 - числа, то определим отображение c1A1 + c2A2 равенством
(c1A1 + c2A2)x = c1A1x + c2A2x (x∈X).
Ясно, что тогда c1A1 + c2A2∈L (X, Y).
(b) Если X, Y, Z - векторные пространства, A∈L(X, Y) и B∈L(Y, Z), то мы определим произведение ВА равенством
(ВА)х = В(Ах) (х∈Х).
Тогда BA∈L(X, Z).
Заметим, что, вообще говоря, ВА≠АВ даже в том случае, когда X = Y = Z.
(с) Нормой ||A|| оператора А∈L (Rn, Rm) называется верхняя грань множества всех чисел 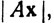 где х пробегает множество всех векторов пространства Rn, таких, что
где х пробегает множество всех векторов пространства Rn, таких, что 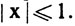
Отметим, что неравенство
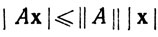
выполняется при всех x∈Rn. Кроме того, если λ таково, что 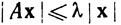 при всех х∈Rn, то
при всех х∈Rn, то 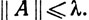
9.7. Теорема. (а) Если A∈L(Rn, Rm), то 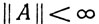 и А - равномерно непрерывное отображение пространства Rn в пространство Rm.
и А - равномерно непрерывное отображение пространства Rn в пространство Rm.
(b) Если A, B∈L(Rn, Rm), а с - число, то
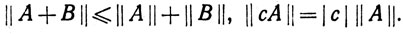
Если расстояние между А и В определить как ||А - В||, то L(Rn, Rm) становится метрическим пространством.
(с) Если A∈L(Rn, Rm) и B∈L(Rm, Rk) то
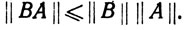
Доказательство.(а) Пусть {е1, ..., еn} - стандартный базис в Rn, и пусть х = ∑ciei, 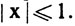 , так что |сi|≤1 при i = 1, ..., n. Тогда
, так что |сi|≤1 при i = 1, ..., n. Тогда
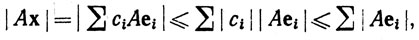
так что
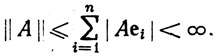
Мы видим, что отображение A равномерно непрерывно, так как 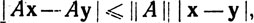 если х, y∈Rn. Неравенство в (b) следует из того, что
если х, y∈Rn. Неравенство в (b) следует из того, что
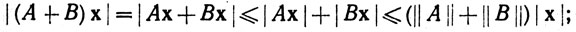
вторая часть утверждения (b) проверяется тем же способом. Если
A, B, C∈L(Rn, Rm),
то выполняется неравенство треугольника
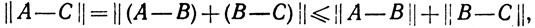
и легко проверить, что ||A-В|| обладает остальными свойствами расстояния (определение 2.17).
Наконец, (с) следует из неравенства
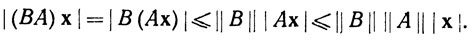
Имея в пространстве L(Rn, Rm) метрику, мы можем перенести на это пространство такие понятия, как непрерывность, открытое множество и т. д. Наша следующая теорема использует эти понятия.
9.8. Теорема. Пусть Ω - множество всех обратимых линейных операторов на Rn.
(a) Если A∈Ω, 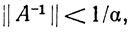 B∈L(Rn) и
B∈L(Rn) и 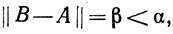 то B∈Ω.
то B∈Ω.
(b) Ω - открытое подмножество пространства L(Rn), и отображение А→A-1 непрерывно на Ω. (Оно, очевидно, взаимно однозначно отображает множество Ω на себя и является обратным к самому себе.)
Доказательство. Из того что 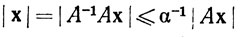 при всех x∈Rn, следует, что
при всех x∈Rn, следует, что
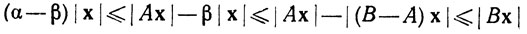
при всех х∈Rn. Это показывает, что оператор В взаимно однозначен, значит, B∈Ω по теореме 9.5. Но это верно при любом В, для которого ||В - A||<α; поэтому множество Ω открыто.
Заменяя в приведенном выше неравенстве х вектором В-1у, получим
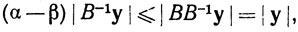
так что 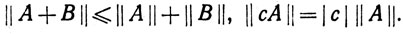 Тождество
Тождество
B-1-A-1 = B-1(A-B)A-1
и теорема 9.7 (с) показывают теперь, что
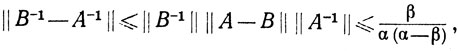
и тем самым доказано утверждение о непрерывности, так как β→0 при В→А.
9.9. Матрицы. Пусть {х1, ..., хn} и {у1, ..., уm} - базисы векторных пространств X и Y соответственно. Тогда любому преобразованию A∈L(X, Y) соответствуют числа аij, такие, что
(1)
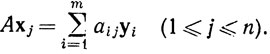
Удобно представлять себе эти числа расположенными в прямоугольную таблицу из m строк и n столбцов, называемую матрицей:
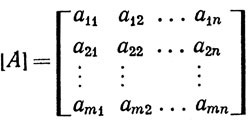
Заметим, что координаты aij вектора Axj (по отношению к базису {у1, ...,уm}) находятся в j-м столбце матрицы [А]. Используя эту терминологию, можно сказать, что множество значений преобразования А натянуто на векторы-столбцы матрицы [А].
Если х = ∑ cjxj, то, в силу линейности преобразования A и равенства (1), получаем
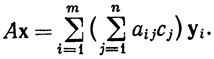
Таким образом, i-я координата вектора Ах равна 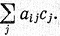
Заметим, что в (1) суммирование производится по первому индексу элемента aij, тогда как, вычисляя координаты, мы суммируем по второму индексу.
Пусть теперь дана матрица из m строк и n столбцов с вещественными элементами aij. Если отображение А определить равенством (2), то ясно, что A∈L(X, Y) и что [А] - исходная матрица. Таким образом, имеется взаимно однозначное соответствие между множеством L(X,Y) и множеством всех вещественных матриц из m строк и n столбцов. Подчеркнем, однако, что [А] зависит не только от A, но и от выбора базисов в X и в У. Одно и то же преобразование А порождает различные матрицы, если менять базисы, и обратно. Мы не станем развивать эту мысль, так как мы обычно будем иметь дело с фиксированными базисами. (Некоторые замечания по этому поводу можно найти в п. 9.26.)
Если Z - третье векторное пространство с базисом {z1, ..., zp}, если А задано равенством (1) и если
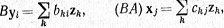
то
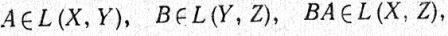
и так как
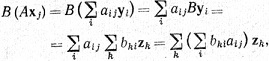
то из независимости множества {z1, ..., zp} следует, что
(3)
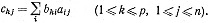
Это показывает, как найти матрицу [ВА] из р строк и n столбцов, зная матрицы [В] и [A]. Если мы определим произведение [В][А] как [ВА], то равенство (3) описывает обычное правило перемножения матриц.
Наконец, допустим, что {х1, ..., хn} и {у1, ..., уm} - стандартные базисы пространств Rn и Rm и что А задано равенством (2). Неравенство Шварца показывает, что
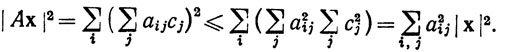
Таким образом,
(4)
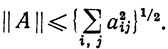
Применяя (4) к В-А вместо А, где A, B∈L(Rn, Rm), мы видим, что если элементы матрицы аij - непрерывные функции некоторого параметра, то то же верно в отношении А. Точнее, если S - метрическое пространство, а11, ..., аmn - вещественные функции, непрерывные на S, и если при любом p∈S Ap - линейное преобразование пространства Rn в пространство Rm, матрица которого составлена из элементов aij (р), то отображение р→Ар - непрерывное отображение пространства S в пространство L (Rn, Rm).
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'