
Упражнения
1. Пусть
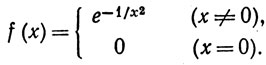
Доказать, что а имеет производные всех порядков в точке x = 0 и что f(n)(0) = 0 при n = 1, 2, 3, ...
2. Доказать следующие предельные соотношения:
(a)
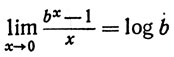
(b&362;0);
(b)
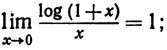
(c)
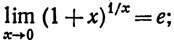
(d)
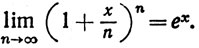
3. Пусть f(x)f(у) = f(x+у) при всех вещественных x и y
(a) Предполагая, что f дифференцируема и отлична от тождественного нуля, доказать, что
f(x) = ecx,
где с - некоторое число.
(b) Доказать то же самое, предполагая, что f только непрерывна.
4. Пусть 0<x<π/2. Доказать, что
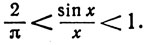
5. Доказать, что при вещественном х и n = 0, 1, 2, ...
|sin nx|≤n|sin x|.
Заметим, что это неравенство может быть неверным для других значений n. Например,
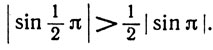
6. Пусть aij - число, стоящее в i-й строке и j-м столбце таблицы

так что
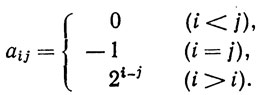
Доказать, что
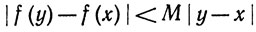
7. Доказать, что
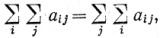
если аij≥0 при всех i и j. (Случай +∞ = +∞ не исключается.)
8. Вывести теорему Вейерштрасса о равномерном приближении многочленами из теоремы Фейера (рассмотреть разложение тригонометрического многочлена в степенной ряд).
9. Будем говорить, что f удовлетворяет условию Липшица в точке х, если существуют числа М и δ>0, такие, что
|f(y) - f(x)|<M|y - x|
при 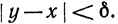
Доказать, что ряд Фурье функции f сходится к f(х) в точке х, если f удовлетворяет условию Липшица в этой точке.
Указание. Функции [f(х - t) - f(x)] Dn(t) равномерно ограничены в интервале (-δ, δ).
10. Если функция f дифференцируема в точке х, то она удовлетворяет условию Липшица в этой точке. Значит, дифференцируемость влечет за собой сходимость ряда Фурье.
11. Пусть

Доказать, что последовательность {rn} сходится. (Ее предел, часто обозначаемый буквой γ, называется эйлеровой постоянной, γ = 0,5772 ... .)
12. Пусть
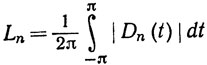
Доказать, что существует число С>0, такое, что
Ln> C log n (n = 1, 2, 3, ...),
или, точнее, что последовательность
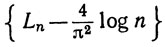
ограничена.
13. Если 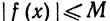 при всех х, то и
при всех х, то и 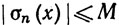 при всех х и n.
при всех х и n.
14. Пусть 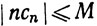 при n = 1, 2, 3, ...,
при n = 1, 2, 3, ...,
sn = c0 + c1 + ... + cn,
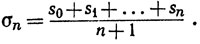
Доказать, что
|sn - σn|≤M.
Указание:
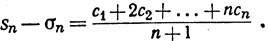
15. Пусть f - функция ограниченной вариации на [-π, π]. Доказать, что если sn есть n-я частная сумма Фурье функции f, то последовательность {sn (x)} равномерно ограничена.
Указание. Воспользоваться двумя предыдущими результатами и упражнением 12 к гл. 6.
16. Доказать, что существует постоянная М, такая, что
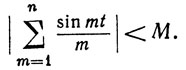
Указание. Применить результат упражнения 15 к ряду Фурье функции
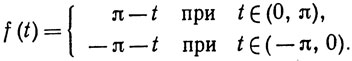
17. Пусть f - функция ограниченной вариации на [-π, π]. Доказать, что если при некотором х
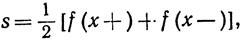
то ряд Фурье функции f сходится в точке х к s.(Эта теорема принадлежит Дирихле.)
Указание. Допустим, не ограничивая общности, что s = 0, х = 0 и f - четная (для нечетной f положим sn (f; 0) = 0 и f(0) = 0). Тогда f непрерывна в нуле. Выберем δ>0 так, чтобы полная вариация функции f на [0, δ] была мала, проинтегрируем по частям и применим упражнение 16, чтобы убедиться в малости интеграла
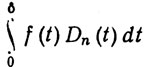
при всех n, а затем воспользуемся теоремой о локализации.
18. Доказать локальный вариант теоремы Фейера: если f∈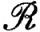 и если функция f непрерывна в точке х0, то σn (f; х0)→f(x0) при n→#8734;.
и если функция f непрерывна в точке х0, то σn (f; х0)→f(x0) при n→#8734;.
19. Пусть аn = ni/n-1, a bn = log n/n. Найти
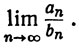
20. Пусть f - функция, непрерывная на R1, f(x + 2π) = f(x) и α/π - иррациональное число. Доказать, что
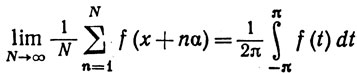
при всех х.
Указание. Сначала доказать это для f(x) = eikx.
21. Сформулировать и доказать теорему о равномерном приближении непрерывной функции интегралами вида
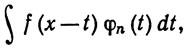
которая содержала бы теоремы Вейерштрасса (7.24) и Фейера (8.15) как частные случаи.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'