Ряды Фурье

8.9. Определение. Тригонометрическим многочленом называется конечная сумма вида

(59)

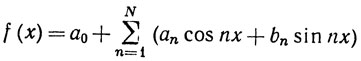
(x вещественно),

где а₀, ..., a_N, b₁, ..., b_N - комплексные числа. Учитывая тождества (46), функцию (59) можно записать в виде

(60)

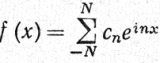
(x вещественно),

который для многих целей более удобен. Ясно, что каждый тригонометрический многочлен - периодическая функция с периодом 2π.

Если π - отличное от нуля целое число, то e^inx - производная функции ^einx/_in, которая тоже имеет период 2π. Поэтому

(61)

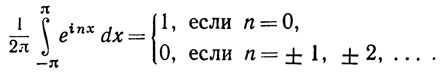
Умножим (60) на е^-imх, где m - целое число; интегрируя это произведение, получим на основании (61)

(62)

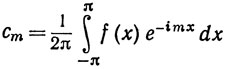
при |m|≤N. Если |m|>N, то интеграл в (62) равен нулю.

Из равенств (60) и (62) видно, что тригонометрический многочлен f, заданный равенством (60), оказывается вещественным в том и только в том случае, когда c_-n = с_n при n = 0, ..., N.

В соответствии с (60) мы определяем тригонометрический ряд как ряд вида

(63)

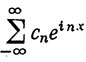
(x вещественно);

N-я частная сумма ряда (63) по определению равна правой части равенства (60).

Если f - функция, интегрируемая на [-π, π], то числа с_m, заданные равенством (62) для всех целых чисел m, называются коэффициентами Фурье функции f, а ряд (63), составленный при помощи этих коэффициентов,- рядом Фурье функции f. Теперь возникает естественный вопрос: сходится ли ряд Фурье функции f к f, или, более общо, определяется ли функция f своим рядом Фурье. Иначе говоря, если мы знаем коэффициенты Фурье функции, то можем ли мы найти эту функцию, и если можем, то как?

Изучение таких рядов и, в частности, проблема представления заданной функции тригонометрическим рядом, имеет своим источником такие разделы физики, как теория колебаний и теория распространения тепла (книга Фурье "Аналитическая теория теплоты" была опубликована в 1822 г.). Многочисленные трудные и тонкие проблемы, возникшие при этом изучении, вызвали основательный пересмотр и перестройку всей теории функций вещественной переменной. Многие выдающиеся имена, и среди них имена Римана, Кантора и Лебега, тесно связаны с этой областью, о которой вполне можно сказать, что в наши дни она вместе со всеми ее обобщениями и ответвлениями занимает центральное положение в анализе.

Мы ограничимся некоторыми основными теоремами, для доказательства которых достаточны методы, развитые в предшествующих главах. Для более основательного исследования естественным и необходимым средством служит интеграл Лебега.

Сначала мы изучим более общие системы функций, обладающие свойством, аналогичным (61).

8.10. Определение. Пусть {φ_n} (n = 1, 2, 3, ... - последовательность комплексных функций на [а, b], такая, что

(64)

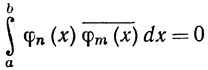
Тогда {φ_n} называется ортогональной системой функций на [а, b]. Если, кроме того,

(65)

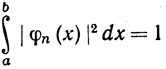
при всех n, то система {φ_n} называется ортонормальной.

Например, функции (2π)^-1/₂e^inx образуют ортонормальную систему на [-π, π]. Таковы же и вещественные функции

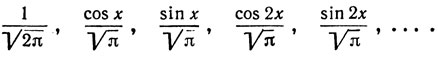
Если {φ_n} - ортонормальная система на [а, b] и если

(66)

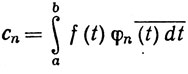
то мы будем называть число с_n n-м коэффициентом Фурье функции f относительно системы {φ_n}. Мы будем писать

(67)

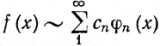
и будем называть этот ряд рядом Фурье функции f (относительно системы {φ_n}).

Заметим, что, употребляя в (67) символ ~, мы ничего не предполагаем о сходимости ряда; этот символ означает только, что коэффициенты задаются равенствами (66).

Следующие теоремы показывают, что частные суммы ряда Фурье функции f обладают некоторым свойством минимальности. Мы будем предполагать здесь, как и на протяжении всей остальной части главы, что f∈, хотя это условие может быть ослаблено.

8.11. Теорема. Пусть система {φ_n} ортонормальна на [а, b]. Пусть

(68)

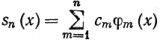
есть n-я частная сумма ряда Фурье функции f, и пусть

(69)

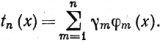
Тогда

(70)

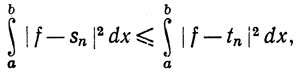
и равенство имеет место тогда и только тогда, когда

(71)

γ_m = c_m (m = 1, ..., n).

Иначе говоря, среди всех функций t_n функция s_n дает наилучшее среднеквадратичное приближение к функции f.

Доказательство. Пусть ∫ обозначает интеграл по сегменту [а, b], ∑ - сумму от 1 до n. Тогда

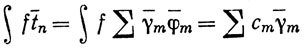
по определению {с_m},

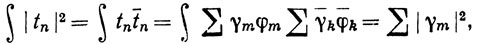
так как система {φ_m} ортонормальна, и поэтому

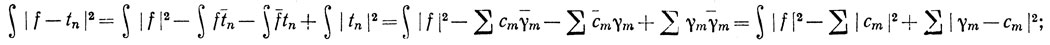
последнее выражение достигает минимума тогда и только тогда, когда γ_m = c_m.

Если в этой выкладке считать γ_m = c_m, то мы получим

(72)

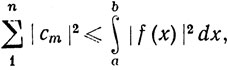
так как ∫|f - t_n|²≥0.

8.12. Теорема. Если {φ_n} - ортонормальная система на [а, b] и если

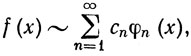
то

(73)

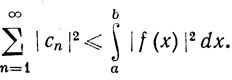
В частности,

(74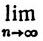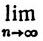) c_n = 0.

Доказательство. Полагая в (72) n→∞, мы получаем неравенство (73) - так называемое "неравенство Бесселя".

Для тригонометрического ряда Фурье, т. е. для ряда (63), коэффициенты которого определяются из (62), неравенство (73) принимает вид

(75)

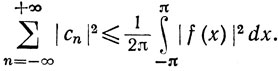
Впоследствии мы увидим, что на самом деле в (75) имеет место равенство.

При изучении тригонометрических рядов Фурье мы встретимся с двумя тригонометрическими многочленами:

(76)

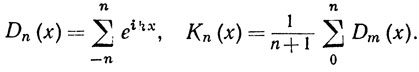
Первый из них называют ядром Дирихле, а второй - ядром Фейера.

8.13. Теорема. При n = 0, 1, 2, ... имеем

(77)

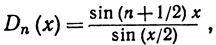
(78)

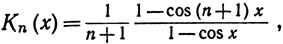
(79)

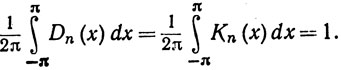
Кроме того, К_n(х)≥0 и

(80)

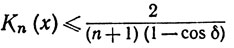
(0<δ≤|x|≤π).

Доказательство. Согласно (76),

(81)

Чтобы получить (77), умножим обе части равенства (81) на e^-ix/₂. Подставляя (81) в определение ядра К_n, получаем

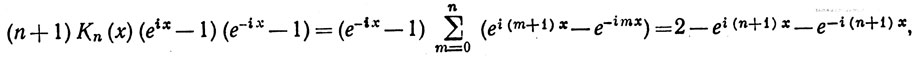
откуда следует (78). Значит, К_n>0 и выполняется (80); (79) следует непосредственно из (76).

Начиная с этого места мы будем иметь дело только с тригонометрической системой. Предположим, что функция f, первоначально определенная на [-π, π], продолжена на R¹ как 2π - периодическая функция^*.

^* (Такое продолжение невозможно, если f(-π)≠f(π), однако функция 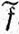, такая, что 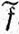(х) = f(х) (х∈(-π, π)) и 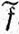(-π) = 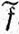(π) = 0, уже может быть продолжена с периодом 2π на всю ось, а ее коэффициенты Фурье, как легко видеть, равны соответствующим коэффициентам функции f.- Прим. перев.)

Коэффициенты Фурье функции f задаются равенством (62); значит, n-я частная сумма s_n ее ряда Фурье равна

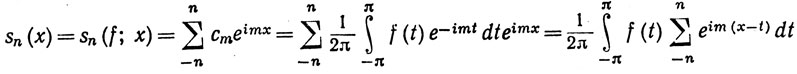
Иными словами,

(82)

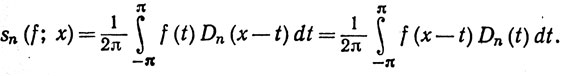
Вследствие периодичности всех участвующих в этом равенстве функций безразлично, по какому интервалу мы будем интегрировать, лишь бы его длина была равна 2π. Именно поэтому и равны интегралы в (82).

8.14. Теорема. Если f∈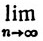 на [-π, π] и 0<δ<π, то

(83)

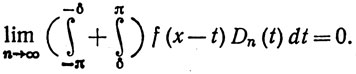
Обычно это равенство называют теоремой о локализации. Оно показывает, что поведение последовательности {s_n(x)}, поскольку речь идет о сходимости, зависит только от значений функции f, принимаемых в некоторой (произвольно малой) окрестности точки х. Таким образом, два ряда Фурье могут вести себя одинаково в одном интервале, а в некотором другом интервале вести себя совершенно по-разному. Мы сталкиваемся здесь с замечательным контрастом между рядами Фурье и степенными рядами (теорема 8.5).

Доказательство. Зафиксируем х, и пусть g(t) = 0 при |t|<δ,

(84)

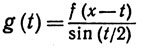
(δ≤|t|≤π).

Согласно (77),

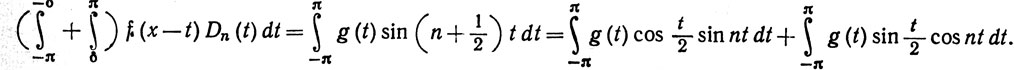
Оба последних интеграла стремятся к нулю при n→∞ согласно (74), так как функции g(t)cos(^t/₂) и g(t)sin(^t/₂) интегрируемы. Отсюда и следует (83).

Таким образом, изучение сходимости последовательности {s_n (f; х)} сводится к изучению интеграла

(85)

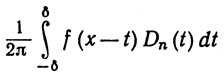
при сколь угодно малом δ>0. Известны несколько достаточных условий сходимости ряда Фурье; доказательства двух из них намечены в упражнениях 9 и 17. Нельзя, очевидно, ожидать, что ряд Фурье любой функции будет сходиться к значению этой функции в любой точке. Действительно, если значения двух функций отличаются только в конечном множестве точек, то интегралы, определяющие их коэффициенты Фурье, будут одинаковыми, и, значит, такие функции имеют один и тот же ряд Фурье.

Здесь имеются трудные проблемы. Не известно даже, верно или нет следующее невинно звучащее утверждение: "для любой непрерывной функции f существует точка х, в которой ряд Фурье функции f сходится". Известно, что существуют непрерывные функции, ряд Фурье которых расходится на несчетном множестве точек. Однако положение весьма улучшается при рассмотрении вместо частных сумм s_n (х) их средних арифметических

(86)

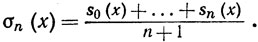
Следующая теорема принадлежит Фейеру.

8.15. Теорема. Если f непрерывна (и, конечно, периодична с периодом 2π) и если {σ_n} - последовательность средних арифметических частных сумм ряда Фурье функции f, то

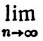σ_n(x) = f(x)

равномерно на R¹.

Заметим по этому поводу, что из теоремы Стона-Вейерштрасса следует существование некоторой последовательности тригонометрических многочленов, равномерно сходящейся к f. Действительно, отождествляя точки х и х+2π, мы можем считать, что периодические функции определены на единичной окружности К. Тригонометрические многочлены, т. е. функции вида (60). образуют алгебру функций на К, удовлетворяющую предположениям теоремы 7.31.

Доказательство. Согласно (86), (82) и (76), имеем

(87)

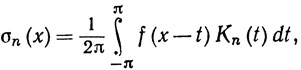
и потому из (79) следует, что

(88)

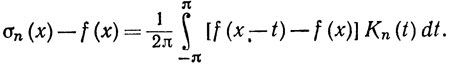
Пусть дано ε>0. Выберем М так, что |f(х)|≤М при всех х. Ввиду того что функция f равномерно непрерывна, мы можем выбрать δ>0 так, что из |х - y|<δ следует

(89)

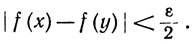
Согласно (80), мы можем затем выбрать N так, чтобы из n≥N и δ≤|t|≤π следовало

(90)

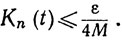
Из (89) следует, что

(91)

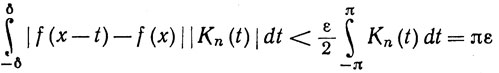
при всех n, так как K_n(t)>0, а из (90) получаем

(92)

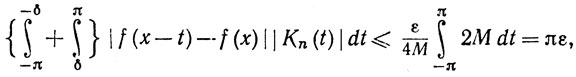
как только n≥N. Наконец, комбинируя (88), (91) и (92), получаем

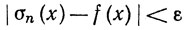
при всех х и всех n≥N. Доказательство закончено.

Заметим, что если бы мы попытались доказать то же самое для s_n(x) вместо σ_n(х), т. е. если бы мы заменили K_n(t) ядром D_n(t), то мы столкнулись бы с интегралом

(94)

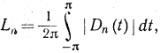
который стремится к ∞ при n→∞. (Упражнение 12.)

Именно этим свойством ядер D_n вызваны трудности, встречающиеся в теории сходимости рядов Фурье.

Следствие 1. Если две непрерывные 2π - периодические функции f и g имеют один и тот же ряд Фурье, то f(x) = g(x) при всех х.

Действительно, если σ_n(х) - среднее арифметическое для этого ряда Фурье, то σ_n(х)→f (x), σ_n(x)→g(x) при каждом х.

Следствие 2. Если функция f непрерывна и если

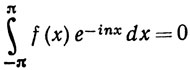
при любом целом n, то f(x) = 0 при всех х.

Это вытекает из следствия 1, если положить там g = 0.

8.16. Теорема. Пусть функции f и g непрерывны (и периодичны с периодом 2π) и

(95)

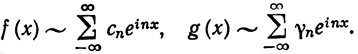
Если s_n есть n-я частная сумма ряда Фурье функции f, то

(96)

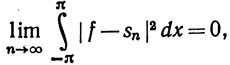
(97)

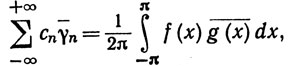
(98)

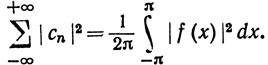
Это утверждение известно как теорема Парсеваля.

Доказательство. Пусть задано число ε>0. Теорема Фейера показывает, что существует N, такое, что |f(x) - σ_n(x)|<ε при всех х и при всех n>N. По теореме 8.11

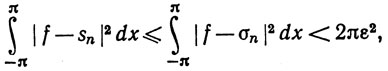
если n>N, и тем самым доказано (96). Далее,

(99)

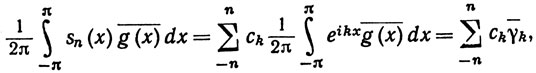
и неравенство Шварца показывает, что

(100)

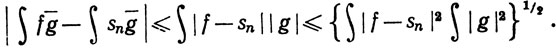
Произведение в фигурных скобках стремится к нулю при n→∞, согласно (96). Сравнивая (99) и (100), получаем (97). Наконец, (98) - это частный случай (f = g) равенства (97).

Условие непрерывности в этой теореме может быть значительно ослаблено. Окончательный вариант теоремы 8.16 будет дан в гл. 10.