Алгебраическая замкнутость поля комплексных чисел

Теперь мы в состоянии дать простое доказательство того факта, что поле комплексных чисел алгебраически замкнуто, т. е. что каждый отличный от постоянной многочлен с комплексными коэффициентами имеет комплексный корень.

8.8.Теорема. Пусть а₀, ..., а_n - комплексные числа, n≥1, а_n≠0, 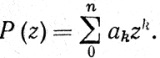Тогда существует такое комплексное число z, что P(z) = 0.

Доказательство. Не ограничивая общности, допустим, что а_n = 1. Положим

(55)

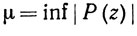
(z - комплексное).

Если |z| = R, то

(56)

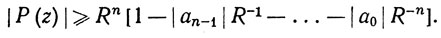
Правая часть неравенства (56) стремится к ∞, когда R→ ∞. Значит, существует такое R₀, что |Р(z)|>μ, если |z|>R₀. Ввиду того что функция |Р| непрерывна на замкнутом круге с центром в нуле радиуса R₀, мы заключаем на основании теоремы 4.16, что |P(z₀)| = 1 при некотором z₀.

Мы утверждаем, что μ = 0.

Если это не так, то положим 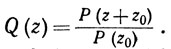Тогда Q - многочлен, отличный от постоянной, Q (0) = 1 и |Q(z)|>1 при всех z. Существует наименьшее целое из всех чисел k, 1≤k≤n, таких, что

(57)

Обозначим это число через k.

По теореме 8.7 (d) существует вещественное θ, такое, что

(58)

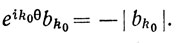
Тогда 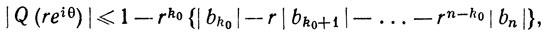если r>0. При достаточно малом r выражение в скобках положительно, значит, |Q (re^iθ)|<1, и мы пришли к противоречию. Таким образом, μ = 0, т. е. P(z₀) = 0.