Тригонометрические функции

Положим, по определению,

Мы покажем, что С(х) и S(x) совпадают с функциями cos x и sin x, определение которых обычно основывается на геометрических рассмотрениях. Согласно (25), 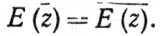Значит, как показывает (46), С(х) и S(x) вещественны при вещественных x. Кроме того,

Таким образом, С(х) и S(x) равны соответственно мнимой и вещественной части числа Е (ix), если x вещественно. Согласно (27),

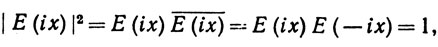
так что

(48)

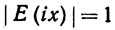
(x вещественно).

Из (46) можно усмотреть, что С(0) = 1, S(0) = 0, а (28) показывает, что

Мы утверждаем, что существуют положительные числа x, такие, что С(x) = 0. Действительно, пусть это не так. Из того, что С(0) = 1, следует тогда, что С(x)>0 при всех x>0; значит, S'(x)>0, согласно (49), и, значит, функция S строго возрастает, а так как S(0) = 0, то S(x)>0 при x>0. Значит, если 0<x<y, то

(50)

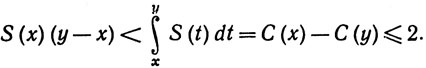
Последнее неравенство следует из (48) и (47). Но (50) не может выполняться при больших у, так как S(x)>0, и мы получили противоречие.

Пусть x₀ - наименьшее из положительных чисел x, таких, что С(x) = 0. Оно существует, так как множество нулей непрерывной функции замкнуто, а С(0)≠0. Определим число я равенством

Тогда С (^π/₂) = 0 и, как показывает (48), S(^π/₂) = ±1. Но так как С(x)>0 в (0, ^π/₂), то S возрастает в (0, ^π/₂); значит, S(^π/₂) = 1. Таким образом,

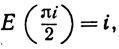
и теорема сложения показывает, что

значит,

8.7.Теорема. (а) Функция Е периодична с периодом 2πi.

(d) Если z - комплексное число, a |z| = 1, то существует единственное число t∈[0, 2π), такое, что Е(it) = z.

Доказательство. Утверждение (а) следует из (53), а утверждение (b) следует из (а) и (46).

Пусть 0<t<^π/₂, а E(it) = x+iy, где x и у вещественны. Сделанное нами ранее показывает, что 0<x<1, 0<y<1. Заметим, что

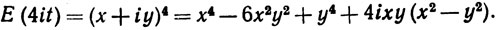
Если Е(4it) вещественно, то х²-у² = 0, а так как, согласно (48), x²+y² = 1, то х² = y² = ¹/₂ , значит, Е(4it) = -1. Тем самым (с) доказано.

Если 0≤t₁<t₂<2π, то

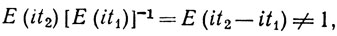
согласно (с). Тем самым доказано утверждение о единственности, содержащееся в (d).

Пусть z₁ = x₁ + iy₁, х₁² + у₁² = 1, x₁≥0, y₁≥0. На [0, ^π/₂] функция С убывает от 1 до 0; значит, C(t₁) = x₁ при некотором t₁ на [0, ^π/₂]. Из того, что C² + S² = 1, a S≥0 на [0, ^π/₂], следует, что z₁ = E (it₁).

Наконец, допустим, что 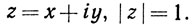Положим z₁ = -iz, если x<0, у≥0. Положим z₁ = -z, если x<0, у<0. Положим z₁ = iz, если x≥0, y<0. Тогда z₁ удовлетворяет предположениям предыдущего абзаца, а так как i = E(^πi/₂), то мы видим, что z = E(i(t₁+^π/₂)) или Е(i(t₁ + π)) или E(i(t₁ + ^3π/₂)), в зависимости от того, какой из трех случаев рассматривается. Тем самым доказано утверждение (d), а с ним вся теорема.

Из (d) и (48) следует, что кривая γ, определенная равенством

- простая замкнутая кривая, множество значений которой - единичная окружность на плоскости. Длина кривой по теореме 6.35 равна

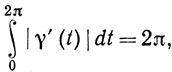
так как γ'(t) = iE(it). Такого результата, конечно, и следовало ожидать для окружности радиуса 1; он показывает, что π, определенное в (51), имеет обычный геометрический смысл.

Таким же точно образом мы увидим что при возрастании t от 0 до t₀ точка γ(t) описывает дугу, лежащую на окружности и имеющую длину t₀. Рассмотрение треугольника с вершинами

показывает, что С(t) и S(t) на самом деле совпадают с cos t и sin t, если эти последние определены обычным способом как отношения сторон прямоугольного треугольника.

Следует подчеркнуть, что мы вывели основные свойства тригонометрических функций из (46) и (25), не привлекая геометрического понятия угла.