Показательная и логарифмическая функции

Положим, по определению,

(25)

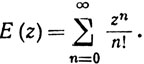
Признак Даламбера показывает, что этот ряд сходится при каждом комплексном z. Применяя теорему 3.50 об умножении абсолютно сходящихся рядов, получаем

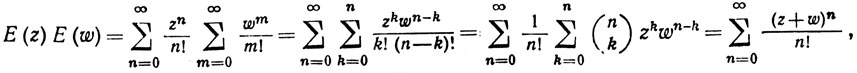
откуда вытекает важная теорема сложения

Одно из ее следствий таково:

Это показывает, что Е(z)≠ при всех z. Согласно (25), Е(х)>0, если х>0; (27) показывает, что Е(х)>0 при всех вещественных х. В силу (25), Е(х)→+∞ при х→+∞, а (27) показывает, что Е(х)→0 при x→-∞ вдоль вещественной оси. В силу (25), из 0<x<y следует, что Е(х)<Е(у); из (27) следует Е(-у)<Е(-х); значит, функция Е строго возрастает на всей вещественной оси.

Теорема сложения показывает также, что

(28)

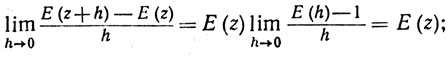
последнее равенство следует прямо из (25). Повторяя (26), получаем

(29)

Положим здесь z₁ = ...= z_n = 1. Поскольку Е(1) = е, где е - число, введенное в определении 3.30, то мы получаем

(30)

Если р = n/m, где n, m - положительные целые числа, то

(31)

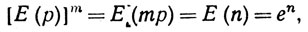
так что

Из (27) следует, что Е(-р) = е^-р, где р - положительное и рациональное. Таким образом, (32) выполняется при всех рациональных р.

В упражнении 7 к гл. 1 мы предложили такое определение:

(33)

где верхняя грань берется по всем рациональным р, таким что p<y для любого вещественного у и х>1. Если&мы таким образом определим при любом вещественном х

то из непрерывности и монотонности функции E, а также из равенства (32) получится

(35)

при всех вещественных х. Равенство (35) объясняет, почему функцию Е называют показательной.

На самом деле вместо (34) вполне можно воспользоваться равенством (35) для определения е^х; равенство (35) - гораздо более удобная отправная точка для исследования свойств функции е^х. Сейчас мы увидим, что и (33) можно заменить более удобным определением (см. (43)).

Вернемся к обычному обозначению е^х вместо Е(x) и подытожим то, что было доказано до сих пор.

8.6.Теорема. Пусть е^х определяется на R¹ равенствами (35) и (25). Тогда

(f) 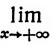xⁿe^-x = 0 при любом n.

Мы уже доказали все утверждения от (а) до (е); (25) показывает, что

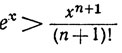
при x>0, так что

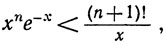
откуда и следует (f). Утверждение (f) означает, что е^х стремится к +∞ при x→+∞ "быстрее", чем любая степень х.

Функция Е, будучи строго возрастающей и дифференцируемой на R¹, имеет обратную функцию L, которая тоже строго возрастает и дифференцируема и область определения которой совпадает с Е(R¹), т. е. с множеством всех положительных чисел. Функция L определяется из равенства

или из равенства

Дифференцируя (37), получаем (ср. с теоремой 5.5)

Записывая у = Е(х), имеем

(38)

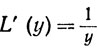
(y>0).

Полагая в (37) x = 0, мы видим, что L(1) = 0. Значит, из (38) следует

(39)

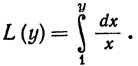
Очень часто равенство (39) принимают за отправную точку в теории логарифма и показательной функции. Полагая u = Е(х), v = E(y), получаем из (26)

так что

Это показывает, что L обладает известным свойством, которое делает логарифмы средством, полезным для вычислений. Обычное обозначение для L(x), конечно, log x.

Что касается поведения функции log x при x→+ ∞ и при x→0, то теорема 8.6 (е) показывает, что

Легко видеть, что

если x>0, а n - целое. Подобным же образом, если m - положительное целое, то

(42)

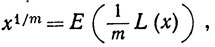
так как каждая из частей равенства (42) после возведения в m-ю степень превращается в соответствующую часть равенства (37). Объединяя (41) и (42), получаем

(43)

при любом рациональном α.

Определим теперь x^α при любом вещественном α и любом x>0 равенством (43). Непрерывность и монотонность функций Е и L показывают, что это определение приводит к тому же результату, что предложенное ранее. Утверждения, сформулированные в упражнениях с 4-го по 7-е гл. 1-тривиальные следствия равенства (43).

Продифференцировав (43), получаем, по теореме 5.5,

(44)

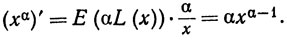
Заметим, что раньше мы использовали (44) только для целых значений α, а в этом случае (44) легко следует из теоремы 5.3 (b).

Доказать равенство (44), исходя непосредственно из определения производной, если x^α определено, как в (33), весьма затруднительно.

Хорошо известная формула интегрирования для х^α следует из (44), если α≠-1, и из (38), если α = -1. Мы хотим доказать еще одно свойство функции log x, а именно

(45)

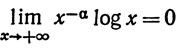
при каждом α>0. Иначе говоря, log x→+∞ при x→+∞ "медленнее", чем любая положительная степень x.

Действительно, если 0<ε<α, а x>1, то

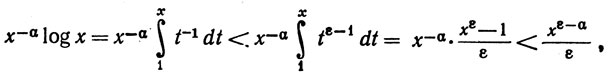
откуда и следует (45). Мы могли бы также воспользоваться теоремой 8.6 (f) для вывода равенства (45).