
Глава 8. Дальнейшие сведения из теории рядов
Степенные ряды
В этом разделе мы изучим некоторые свойства функций, представимых в виде суммы степенного ряда, т. е. функций вида
(1)
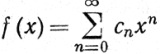
или, более общо,
(2)
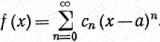
Такие функции называются аналитическими.
Мы ограничимся вещественными значениями х. Поэтому вместо кругов сходимости (см. теорему 3.39) мы будем иметь дело с промежутками сходимости.
Если ряд (1) сходится при всех х из интервала (-R, R) для некоторого R>0 (R может равняться +∞), то мы будем говорить, что функция f разлагается в степенной ряд в окрестности точки х = 0. Аналогично, если ряд (2) сходится при |х-a|<R, то говорят, что f разлагается в степенной ряд в окрестности точки х = а. Для удобства мы часто будем полагать а = 0, не ограничивая общности.
8.1.Теорема. Пусть ряд
(3)
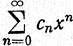
сходится при |х|<R<∞, и пусть
(4)
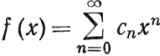
(|x|<R).
Тогда ряд (3) сходится равномерно на отрезке [-R+ε, R-ε], каково бы ни было положительное число ε<R. Функция f непрерывна на (-R, R) и
(5)
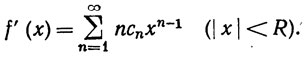
Доказательство. Пусть 0<ε<R. Если |x|≤R-ε, то
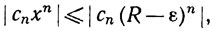
а так как ряд
∑cn(R-ε)n
сходится абсолютно (каждый степенной ряд по признаку Коши сходится абсолютно внутри своего промежутка сходимости), то из теоремы 7.10 следует равномерная сходимость ряда (3) на отрезке [-R+ε, R-ε].
Ввиду того что 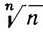 →1 при n→∞, имеем
→1 при n→∞, имеем
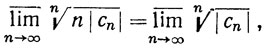
так что ряды (4) и (5) имеют общий интервал сходимости.
Поскольку (5) - степенной ряд, то он сходится равномерно в [-R+ε, R-ε] при каждом положительном ε<R и, следовательно, применима теорема 7.17 (в формулировке теоремы последовательности можно заменить рядами). Таким образом, (5) выполняется, если |x|≤R-ε, можно найти такое число ε>0, что |x|<R-ε. Значит, (5) выполняется, если |x|<R.
Непрерывность функции f следует из существования f' (теорема 5.2).
Следствие. Если выполнены условия теоремы 8.1, то f имеет производные всех порядков в (-R, R), причем
(6)
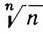
В частности,
(7) f(k)(0) = k!ck (k = 0, 1, 2, ...).
(Здесь f(0) обозначает f, a f(k) k-ю производную функции f при k = 1, 2, 3, ...).
Доказательство. Равенство (6) получится, если мы последовательно применим теорему 8.1 к f, затем к f', к f" и т. д. Полагая в (6) х = 0, мы получим (7).
Формула (7) очень интересна. Она показывает, с одной стороны, что коэффициенты степенного разложения функции f определяются значениями f и ее производных в одной-единственной точке. С другой стороны, если даны коэффициенты, то значения производных функции f в центре интервала сходимости усматриваются непосредственно из степенного ряда.
Заметим, однако, что если даже функция f имеет производные всех порядков, то ряд ∑сnхn, коэффициенты которого вычислены по формуле (7), не обязан сходиться к f(х) ни при каком х ≠ 0. В последнем случае f не может быть разложена в степенной ряд в окрестности точки х = 0. Действительно, если бы выполнялось равенство f(х) = ∑anxn, то мы имели бы
n!an = f(n)(0);
значит, аn = сn. Пример такой ситуации будет дан в упражнении 1.
Если ряд (3) сходится в конце промежутка сходимости, скажем, в точке x = R (и, разумеется, R<∞), то функция f непрерывна не только в интервале (-R, R), но и в точке x = R. Это вытекает из следующей теоремы Абеля (для простоты мы полагаем R = 1).
8.2.Теорема. Пусть ряд ∑cn сходится. Положим
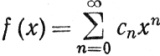
(-1<x<1)
Тогда
(8)
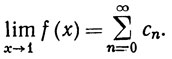
Доказательство. Пусть sn = c0+...+cn, s-1 = 0. Тогда
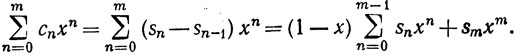
Пусть |x|<1 и m→∞. Так как sm ограничены в совокупности, то мы получаем
(9)
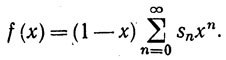
Предположим, что 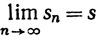 . Пусть ε>0. Выберем N, такое, что из n>N следует
. Пусть ε>0. Выберем N, такое, что из n>N следует
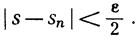
Тогда, ввиду того что
(1-x)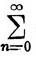 xn = 1 (x|<1).
xn = 1 (x|<1).
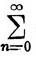 xn = 1 (x|<1).
xn = 1 (x|<1).мы получаем из (9)
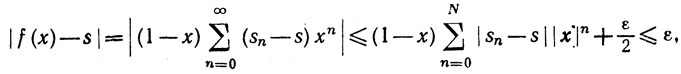
если x>1-δ, где δ - любое достаточно малое положительное число. Отсюда следует (8).
В качестве приложения докажем теорему 3.51, которая состоит в следующем. Если ряды ∑an, ∑bn, ∑cn сходятся соответственно к А, В, С и если сn = a0bn+ ... +anb0, то С = АВ.
Положим
f(x) = 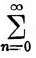 anxn,
g(x) =
anxn,
g(x) = 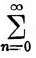 bnxn,
h(x) =
bnxn,
h(x) = 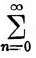 cnxn,
cnxn,
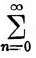 anxn,
g(x) =
anxn,
g(x) = 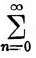 bnxn,
h(x) =
bnxn,
h(x) = 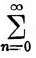 cnxn,
cnxn,при 0≤x≤1. Если х<1, то эти ряды сходятся абсолютно, и поэтому их можно перемножить в соответствии с определением 3.48; выполнив умножение, мы увидим, что
(10)
f(x)*g(x) = h(x) (0≤x<1).
По теореме 8.2
(11)
f(x)→A, g(x)→B, h(x)→C
при х→1. Из равенств (10) и (11) следует, что АВ = С.
Далее нам понадобится следующая теорема об изменении порядка суммирования двойной последовательности.
8.3.Теорема. Пусть дана двойная последовательность {аij}, i = 1, 2, 3, ..., j = 1, 2, 3, ..., пусть
(12)
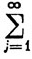 |aij| = bi (i = 1, 2, 3, ...).
|aij| = bi (i = 1, 2, 3, ...).и ряд ∑bi сходится. Тогда
(13)
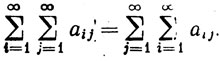
Доказательство. Мы могли бы установить равенство,(13) непосредственно, подобно тому как это было сделано в теореме 3.56 (хотя в данном случае это несколько более сложно). Однако следующий метод представляется более интересным.
Пусть Е - счетное множество, состоящее из попарно различных точек х0, х1, х2, ..., и пусть хn→х0 при n→∞. Положим
(14)
fi(x0) = 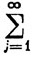 aij (i = 1, 2, 3, ...),
aij (i = 1, 2, 3, ...),
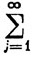 aij (i = 1, 2, 3, ...),
aij (i = 1, 2, 3, ...),(15)
fi(xn) = 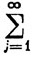 aij (i, n = 1, 2, 3, ...),
aij (i, n = 1, 2, 3, ...),
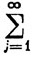 aij (i, n = 1, 2, 3, ...),
aij (i, n = 1, 2, 3, ...),(16)
g(x) = 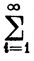 fi(x) (x∈E).
fi(x) (x∈E).
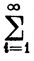 fi(x) (x∈E).
fi(x) (x∈E).Теперь, сопоставляя (14) и (15) с условием (12), мы видим, что каждая из функций fi непрерывна в точке х0. Поскольку |fi(x)|≤bi при х∈Е, ряд (16) сходится равномерно на Е, так что функция g непрерывна в точке х0 (теорема 7.11). Следовательно,
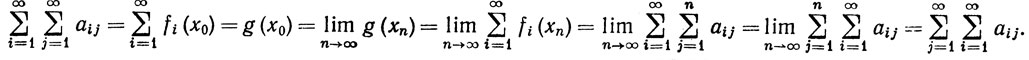
8.4.Теорема. Пусть ряд
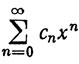
сходится при |x|<R и f(x) - сумма этого ряда в интервале (-R, R). Если -R<a<R, то функцию f можно разложить в степенной ряд в окрестности точки х = а, сходящийся при 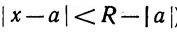 , и
, и
(17)
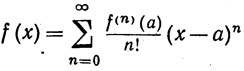
(
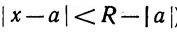 )
)Эта теорема является обобщением теоремы 5.17; она известна также как теорема Тейлора.
Доказательство. Имеем
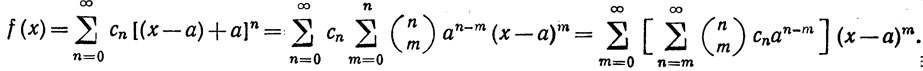
Это и есть нужное нам разложение в окрестности точки х = а. Чтобы убедиться в его справедливости, мы должны обосновать изменение порядка суммирования. Теорема 8.3 показывает, что оно возможно, если ряд
(18)
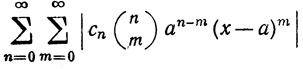
сходится. Но (18), очевидно, приводится к виду
(19)
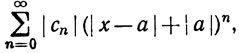
а ряд (19) сходится, если |x-a|+|a|<R.
Наконец, формула (17) для коэффициентов следует из (7). Нужно заметить, что ряд (17) в действительности может сходиться в интервале, более широком, чем интервал, определяемый неравенством 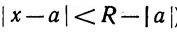 .
.
Если два степенных ряда сходятся в интервале (-R, R) к одной и той же функции, то они тождественны, т. е. их коэффициенты с одинаковыми номерами равны. Интересно, что то же верно и в более слабых предположениях.
8.5.Теорема. Пусть ряды ∑аnхn и ∑bnxn сходятся в интервале S = (-R, R). Пусть Е - множество всех точек x∈S, в которых
(20)
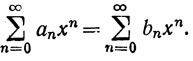
Если Е имеет предельную точку в S, то аn = bn при n = 0, 1, 2, ... . Значит, (20) выполняется и при всех x∈S.
Доказательство. Пусть сn = аn - bn и
(21) f(x) = 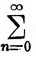 cnxn (x∈)
cnxn (x∈)
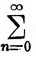 cnxn (x∈)
cnxn (x∈)Тогда f(x) = 0 на Е.
Пусть A - множество всех предельных точек множества E, содержащихся в S, а B - множество всех прочих точек из S. Из определения предельной точки ясно, что множество B открыто. Допустим, что нам удалось доказать, что и А открыто. По условию А непусто. Кроме того, S = А∪B, А∩ B = ∅ и S связно (теорема 2.47). Из определения 2.45 следует, что в таком случае B должно быть пустым и, значит, A = S. Из того, что функция f непрерывна на S, следует А⊂Е. Таким образом, E = S, а (7) показывает, что сn = 0 при n = 0, 1, 2, ..., что и составляет требуемое заключение.
Таким образом, нам нужно доказать, что А открыто. Если х0∈А, то теорема 8.4 показывает, что
(22)
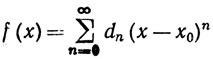
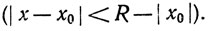
Мы утверждаем, что dn = 0 при всех n. Предполагая противное, обозначим через k наименьшее из неотрицательных целых чисел m, таких, что dm≠0. Тогда
(23)
f(x) = (x-x0)kg(x) 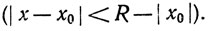
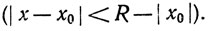
(24)
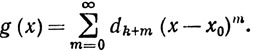
Поскольку функция g непрерывна в точке х0 и
g (x0) = dk≠0,
то существует δ>0, такое, что g(x)≠0, если |х-x0|<δ. Из (23) следует, что f(х)≠0, если 0<|х-х0|<δ. Но это противоречит тому, что х0 - предельная точка множества Е,
Таким образом, dn = 0 при всех n, так что f(x) = 0 при всех дс, для которых выполняется (22), т. е. в окрестности точки х0. Это показывает, что А открыто, и доказательство закончено.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'