
Упражнения
1. Доказать, что всякая равномерно сходящаяся последовательность ограниченных функций равномерно ограничена.
2. Пусть последовательности {fn} и {gn} сходятся равномерно на Е. Доказать, что последовательность {fn + gn} сходится равномерно на Е. Пусть, кроме того, {fn} и {gn} - последовательности ограниченных функций. Доказать, что последовательность {fngn} сходится равномерно на Е.
3. Построить последовательности {fn}, {gn}, которые сходятся равномерно на Е, но {fngn} не сходится равномерно на Е (разумеется, {fngn} сходится на Е).
4. Рассмотрим ряд
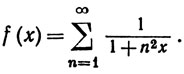
При каких значениях х этот ряд сходится абсолютно? На каких сегментах он сходится равномерно? На каких сегментах он перестает быть равномерно сходящимся? Непрерывна ли функция f в тех точках, в которых ряд сходится? Ограничена ли f?
5. Пусть
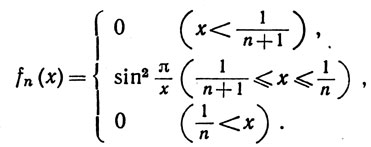
Показать, что последовательность {fn} сходится к непрерывной функции, но неравномерно. Воспользоваться рядом ∑fn для доказательства того, что абсолютная сходимость (даже если она имеет место при всех х) не влечет за собой равномерной сходимости.
6. Доказать, что ряд
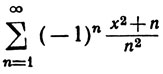
сходится равномерно на каждом ограниченном сегменте, но не сходится абсолютно ни при одном значении х.
7. Положим
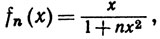
где n = 1, 2, 3, ..., х - вещественное число. Показать, что последовательность {fn} сходится равномерно к функции f и что равенство
f'(x)=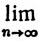 f'n(x)
f'n(x)
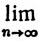 f'n(x)
f'n(x)верно, если х≠0, и неверно, если х = 0.
8. Пусть
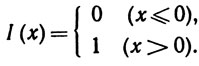
Пусть {xn} - последовательность попарно различных точек интервала (а, b), и пусть ряд 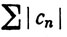 сходится. Доказать, что ряд
сходится. Доказать, что ряд
f(x) = 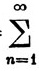 cnI(x-xn) (a≤x≤b)
cnI(x-xn) (a≤x≤b)
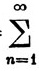 cnI(x-xn) (a≤x≤b)
cnI(x-xn) (a≤x≤b)сходится равномерно, что функция f непрерывна при любом х≠xn и что f - функция ограниченной вариации.
9. Пусть {gn} - последовательность функций ограниченной вариации на сегменте [а, b], обладающая следующим свойством: для любого ε>0 существует такое число N, что из неравенств n≥N, m≥N следует неравенство V(gn - gm)<ε. Доказать, что существует функция g, имеющая ограниченную вариацию на [а, b] и такая, что V (gn - g)→0 при n→∞.
10. Пусть функция f непрерывна на [а, b], и пусть {gn} - последовательность, для которой
(a) V{gn)≤M (n = 1, 2, 3, ...),
(b) 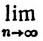 gn(x) = g(x) (a≤x≤b).
gn(x) = g(x) (a≤x≤b).
Доказать, что
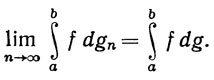
Заметим, что предположение здесь слабее предположений теоремы 7.16.
Указание. Сначала показать, что V(g)≤M. Далее, для любого разбиения Р: а = х0<x1< ... <xm = b имеем
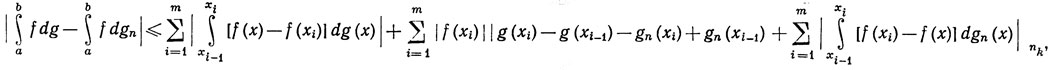
Первая и третья суммы могут быть сделаны сколь угодно малыми за счет выбора μ(P) и непрерывности функции f. Фиксируя Р, получаем, что вторая сумма стремится к нулю при n→∞.
11. Если функция f непрерывна на [0, 1] и если
Указание. Интеграл от произведения функции f на любой многочлен равен нулю. Воспользоваться теоремой Вейерштрасса и показать, что  f2(x)dx = 0.
f2(x)dx = 0.
12. Если, например, 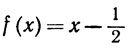 и g(x) = x - x2, то
и g(x) = x - x2, то
(75)
 f(x)[g(x)]ndx = 0 (n = 0, 1, 2, ...).
f(x)[g(x)]ndx = 0 (n = 0, 1, 2, ...).Для каких функций g из условия (75) следует, что f(x) = 0 при всех х∈[0, 1], если заранее задано, что f - непрерывна?
13. Пусть {fn}, {gn} - последовательности функций, определенных на Е, и
(а) частные суммы ряда ∑ fn равномерно ограничены;
(b) gn→0 равномерно на Е;
(с) g1(х)≥g2(х)≥g3(х)≥... при любом х∈Е.
Тогда ряд ∑ fngn сходится равномерно на Е.
Указание. Сравнить с теоремой 3.42.
14. Пусть {fn} - равномерно ограниченная последовательность функций, интегрируемых по Риману на [а, b]. Положим
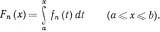
Доказать, что существует подпоследовательность Fnk, равномерно сходящаяся на [а, b].
15. Пусть {fn} - последовательность непрерывных функций, сходящаяся равномерно на множестве Е к функции f. Доказать, что
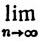 fn(xn) = f(x)
fn(xn) = f(x)для каждой последовательности точек хn∈Е, такой, что хn→х, где x∈E. Верно ли обратное?
16. Пусть (х) обозначает дробную часть вещественного числа х (см. определение в упражнении 2 к гл. 4). Рассмотрим функцию
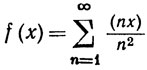
(x - вещественное число).
Найти все точки разрыва функции f и показать, что множество таких точек счетно и всюду плотно. Показать, что (тем не менее) функция f интегрируема по Риману на каждом ограниченном сегменте.
17. Пусть {fn} - последовательность функций, монотонных на [а, b], и пусть {fn} поточечно сходится к функции f, непрерывной на [а, b]. Доказать, что сходимость равномерна на [а, b].
18. Пусть {fn} - равностепенно непрерывная последовательность функций на компактном множестве К, и пусть {fn} сходится поточечно на К. Доказать, что последовательность {fn} сходится равномерно на К.
19. Доказать утверждения о 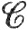 (K), сформулированные в п. 7.32.
(K), сформулированные в п. 7.32.
20. Определить понятия равномерной сходимости и равностепенной непрерывности для отображений в любое метрическое пространство. Показать, что теоремы 7.9 и 7.12 верны для отображений в любое метрическое пространство, что теоремы 7.8 и 7.11 верны для отображений в любое полное метрическое пространство и что теоремы 7.10, 7.14, 7.17 и 7.23 верны для векторнозначных функций, т. е. для отображений в любое Rk.
21. Пусть К - единичная окружность на комплексной плоскости (т. е. множество всех z, таких, что |z| = 1), и пусть 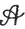 - алгебра всех функций вида
- алгебра всех функций вида
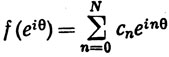
(Θ вещественно).
Тогда 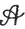 разделяет точки множества К и не исчезает ни в одной точке множества К, но тем не менее существуют непрерывные на К функции, не содержащиеся в равномерном замыкании алгебры
разделяет точки множества К и не исчезает ни в одной точке множества К, но тем не менее существуют непрерывные на К функции, не содержащиеся в равномерном замыкании алгебры 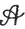 .
.
Указание. Для любой функции f∈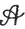
 f(eiΘ)einΘdΘ = 0, n = 1, 2, ... ,
f(eiΘ)einΘdΘ = 0, n = 1, 2, ... ,
и это остается верным для каждой f принадлежащей замыканию алгебры 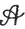 .
.
22. Пусть φ - непрерывная ограниченная вещественная функция, определенная в полосе, выделяемой неравенствами 0≤x≤1, -∞<y<+∞. Доказать, что задача с начальными данными
у' = φ(х, у), у(0) = с
имеет решение. [Заметим, что условия этой теоремы существования менее ограничительны, чем условия соответствующей теоремы единственности (см. упражнение 17 гл. 5).]
Указание. Зафиксируем n. Положим хi = i/n, i = 0, ..., n. Пусть fn - непрерывная функция на [0, 1], такая, что fn(0) = c,
f'n(t) = φ(xi, fn(xi)), если xi<t<xi+1
и положим
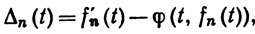
за исключением точек xi, где Δn(t) = 0. Тогда
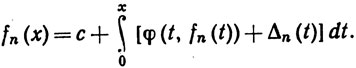
Воспользоваться теоремой 7.23 для доказательства равномерной на [0, 1] сходимости некоторой подпоследовательности последовательности {fn} к функции f, удовлетворяющей интегральному уравнению
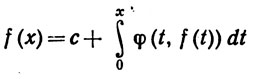
(0≤x≤1).
Эта функция f и есть решение данной задачи.
23. Доказать аналогичную теорему существования для задачи с начальными данными
y' = φ(x, y), y(0) = с,
где теперь c∈Rk, у∈Rk, а φ - непрерывное ограниченное отображение части пространства Rk+1, выделяемой условиями 0≤x≤1, y∈Rk, в пространство Rk. (Сравнить с упражнением 18 гл. 5.)
Указание. Воспользоваться "векторнозначным" вариантом теоремы 7.23.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'