Теорема Стона - Вейерштрасса

7.24. Теорема. Если f - непрерывная комплексная функция на [а, b], то существует такая последовательность многочленов Р_n, что

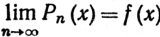
равномерно на [а, b]. Если функция f вещественна, то и многочлены Р_n можно выбрать вещественными.

Именно в такой форме эта теорема была первоначально открыта Вейерштрассом.

Доказательство. Не ограничивая общности, мы можем считать, что [а, b] = [0, 1]. Будем считать также, что f(0) = f(1) = 0. Действительно, если теорема доказана для этого случая, то рассмотрим

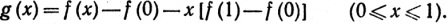
Здесь g(0) = g(1) = 0, и если g представима в виде предела равномерно сходящейся последовательности многочленов, то такова и f, так как f-g - многочлен. Будем считать, что f(x) = 0 вне сегмента [0, 1]. Тогда функция f равномерно непрерывна на всей вещественной прямой. Положим

(58)

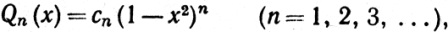
где с_n выбраны так, что

(59)

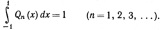
Нам нужны некоторые сведения о порядке величины с_n. Ввиду того что

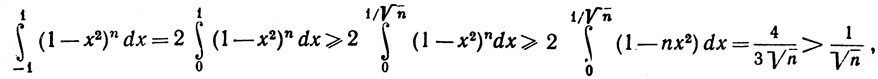
из (59) следует, что

(60)

Неравенство (1 - х²)ⁿ≥1 - nx², которым мы воспользовались выше, легко проверяется. Для этого нужно рассмотреть функцию

которая равна нулю при x = 0 и имеет положительную производную в (0,1).

При любом δ>0 из (60) следует, что

(61)

Q_n(x)≤√n(1 - δ²)ⁿ ()

так что Q_n→0 равномерно в сегменте Положим теперь

(62)

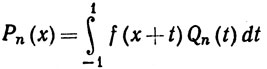
(0≤x≤1).

Наши предположения о функции f показывают (с помощью простой замены переменной), что

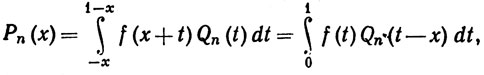
а последний интеграл, очевидно, есть многочлен по х. Таким образом, {Р_n} - последовательность многочленов, причем вещественная, если вещественна функция f. Задав ε>0, выберем δ>0 так, чтобы из |у-х|<δ следовало

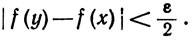
Пусть M = sup|f(x)|. Используя (59), (61) и тот факт, что Q_n(x)≥0, мы видим, что при 0≤x≤1

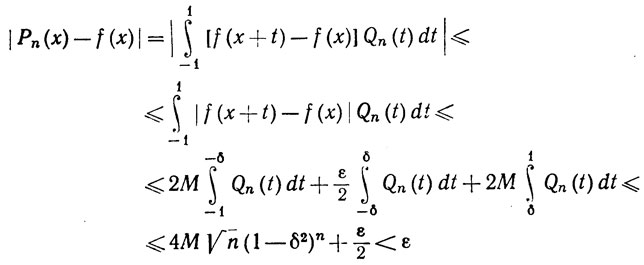
при всех достаточно больших n. Теорема доказана.

Поучительно набросать графики функций Q_n для нескольких значений n. Отметим еще, что равномерная непрерывность функции f была нам нужна для доказательства равномерной сходимости последовательности {Р_n}.

При доказательстве теоремы 7.30 нам не потребуется теорема 7.24 в полном объеме, а потребуется только один ее частный случай, который мы сформулируем в виде следствия.

7.25. Следствие.Для любого сегмента [-а, а] существует последовательность вещественных многочленов Р_n, такая, что Р_n(0) = 0 и

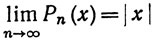
равномерно на [-а, а].

Доказательство. По теореме 7.24 существует последовательность {Р_n} вещественных многочленов, сходящаяся к |х| равномерно на [-а, а]. В частности, Р^*_n(0)→0 при n→∞. Многочлены

обладают нужными свойствами.

Теперь мы выделим те свойства многочленов, на которых основана теорема Вейерштрасса.

7.26. Определение. Совокупность комплексных функций, определенных на множестве Е, называется алгеброй, если (i) f+g∈, (ii) fg∈, и (iii) cf∈ при всех f∈, g∈ и всех комплексных постоянных с. Иными словами, множество - замкнуто относительно сложения, умножения и умножения на скаляры.

Мы будем рассматривать также алгебры вещественных функций; в этом случае в (iii) речь идет, конечно, об умножении лишь на вещественные с.

Множество функций, обладающее тем свойством, что f∈, если f_n∈ (n = 1, 2, 3,...) и f_n→f равномерно на Е, называется равномерно замкнутым.

Пусть - множество всех функций, которые служат пределами равномерно сходящихся на множестве Е последовательностей элементов множества . Тогда J5 называется равномерным замыканием множества .

Например, множество всех многочленов - алгебра, и теорему Вейерштрасса можно сформулировать так: множество всех функций, непрерывных на [а, b], есть равномерное замыкание множества всех многочленов на [а, b].

7.27. Теорема. Пусть - равномерное замыкание алгебры , состоящей из ограниченных функций. Тогда - равномерно замкнутая алгебра.

Доказательство. Если f∈ и g∈, то существуют равномерно сходящиеся последовательности {f_n}, {g_n}, такие, что f_n→f, g_n→g и f_n∈, g_n∈. Пользуясь тем, что мы имеем дело с ограниченными функциями, легко показать, что

где с - любая постоянная, причем сходимость равномерна во всех трех случаях.

Значит, f+g∈, fg∈ и cf∈, так что -алгебра. Пусть {f_n} - равномерно сходящаяся последовательность элементов алгебры . Существуют функции g_n∈ такие, что

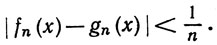
Если f_n→f равномерно, то ясно, что и g_n→f равномерно, так что f∈ и равномерно замкнуто.

7.28. Определение. Пусть - множество функций, определенных на множестве Е. Тогда говорят, что разделяет точки множества Е, если для каждой пары различных точек х₁, х₂∈Е найдется функция f∈, такая, что f(x₁)≠f(x₂).

Если для каждой точки х∈Е найдется функция g∈E, такая, что g(x)≠0, то мы будем говорить, что алгебра не исчезает ни в одной точке множества Е.

Алгебра всех многочленов от одной переменной, очевидно, обладает этими свойствами на R¹. Примером алгебры, не разделяющей точек, служит множество всех четных многочленов, рассматриваемых, скажем, на [- 1, 1], так как f(-x) = f(x) для каждой четной функции f.

Следующая теорема иллюстрирует эти понятия.

7.29. Теорема. Пусть - алгебра функций на множестве Е, разделяет точки и не исчезает ни в одной точке множества Е. Пусть x₁, х₂ - различные точки множества Е и с₁, с₂ - постоянные (вещественные, если - вещественная алгебра). Тогда содержит функцию f, такую, что

Доказательство. Наши предположения показывают, что содержит функции g и h, такие, что g(x₁)≠g(х₂) и h(x₁)≠0. Положим

где λ - постоянная, выбранная следующим образом: если g(x₁)≠0, то λ = 0; если g(x₁) = 0, то g(x₂)≠0, и существует число λ≠0, такое, что

Тогда u∈ и наш выбор λ показывает, что u(x₁)≠u(x₂) и u(х₁)≠0. Если

то α≠0; если

то f₁∈, f₁(x₁) = 1, f₁(x₂) = 0.

Подобным же образом мы проверим, что существует функция f₂∈, такая, что f₂(x₁) = 0, f₂(x₂) = 1. Тогда функция f = c₁f₁ + c₂f₂ обладает нужными свойствами.

Теперь мы докажем теорему Стона, обобщающую теорему Вейерштрасса.

7.30. Теорема. Пусть -алгебра вещественных непрерывных функций на компактном множестве К. Если разделяет точки множества К и не исчезает ни в одной точке множества К, то равномерное замыкание алгебры содержит все функции, непрерывные на К.

Мы разобьем доказательство на четыре шага.

Первый шаг. Если f∈, то |f|∈.

Доказательство. Пусть

(63)

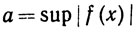
(x∈K)

и пусть задано число ε>0. Согласно следствию 7.25, существуют вещественные числа c₁, ..., с_n, такие, что

(64)

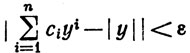
(-a≤y≤a).

Функция g = 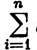c_ifⁱ входит в состав множества , так как - алгебра. Согласно (63) и (64), мы имеем

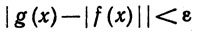
(x∈K).

Поскольку алгебра равномерно замкнута, то отсюда следует, что |f|∈.

Второй шаг. Если f∈ и g∈, то mах(f, g)∈ и min (f,g)∈.

При этом h = max (f, g) означает, что

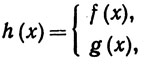
min(f, g) определяется аналогично.

Доказательство. Наше утверждение следует из доказанного на первом шаге и из тождеств

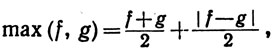
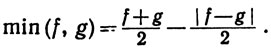
Разумеется, этот результат можно по индукции распространить на любое конечное множество функций: если f₁, ...,f_n∈, то max(f₁, ...,f_n)∈ и min(f₁, ...,f_n)∈.

Третий шаг. Пусть заданы вещественная функция f, непрерывная на K, точка х∈К и ε>0. Тогда найдется функция g_x∈ такая, что g_x(x) = f(x) и

Доказательство. Поскольку ⊂ и удовлетворяет условиям теоремы 7.29, то и удовлетворяет этим условиям. Значит, для любого у∈К можно найти функцию h_y∈, такую, что

(66)

В силу непрерывности функции h_y, существует открытое множество J_у, содержащее точку у и такое, что

(67)

Ввиду того что К - компакт, имеется конечное множество точек y₁, ..., у_n, таких, что

(68)

Положим

Согласно установленному на втором шаге, g_x∈, а из соотношений (66)-(68) следует, что g_x обладает и остальными нужными свойствами.

Четвертый шаг. Пусть заданы вещественная функция f, непрерывная на К, и ε>0. Существует функция h∈, такая, что

(69)

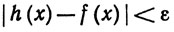
Это утверждение равносильно утверждению теоремы, так как равномерно замкнута.

Доказательство. Рассмотрим функции g_x, построенные на третьем шаге для каждого х∈К. В силу непрерывности функции g_x, существует открытое множество V_x, содержащее х и такое, что

(70)

Ввиду того что К компактно, существует конечное множество точек х₁, ..., х_n, таких, что

(71)

Положим h = min(g_x1, ...,g_xm). Как было установлено на втором шаге, h∈, и из (65) следует, что

(72)

С другой стороны, из (70) и (71) следует, что

(73)

Из (72) и (73) вытекает (69).

Теорема 7.30 не верна для произвольных комплексных алгебр. Контрпример дан в упражнении 21. Однако утверждение теоремы остается верным даже и для комплексных алгебр, если на наложить еще одно условие, а именно если потребовать, чтобы была самосопряженной. Это означает, что для любой функции f∈ комплексно-сопряженная с ней функция 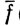тоже принадлежит функция 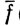определяется равенством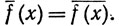

7.31. Теорема. Пусть - самосопряженная алгебра комплексных непрерывных функций на компактном множестве К. Пусть -разделяет точки множества К и не исчезает ни в одной точке множества К. Тогда равномерное замыкание алгебры содержит все комплексные непрерывные на К функции.

Доказательство. Пусть _R - множество всех вещественных функций на К, принадлежащих алгебре . Если f∈ и f = u+iv, где u, v - вещественны, то 2u = f+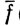, а так как - самосопряженная алгебра, то u∈_R. Если х₁≠x₂, то существует f∈, такая, что f(x₁) = 1, f(х₂) = 0; значит, 0 = u(х₂)≠u(х₁) = 1, откуда следует, что _R разделяет точки множества К. Если х∈K, то g(x)≠0 при некотором g∈ и имеется комплексное число X, такое, что λg(x)>0; если f = λg, f = u+iv, то отсюда следует, что u(х)>0; значит, _R не исчезает ни в одной точке множества К.

Таким образом, _R удовлетворяет условиям теоремы 7.30. Следовательно, каждая вещественная непрерывная на К функция принадлежит равномерному замыканию алгебры R_, т. е. принадлежит . Если f - комплексная непрерывная на К функция, f = u+iv, то u∈, v∈, значит, и f∈. Доказательство закончено.

7.32. Замечания. Пусть (К) обозначает множество всех вещественных непрерывных функций на компактном пространстве К. Определим норму функций f∈(К) равенством

(74)

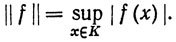
По теореме 4.15 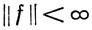при каждом f∈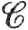(К). Очевидно, что

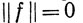
только тогда, когда f(x) = 0 при всех х∈К, т. е. f = 0, и нетрудно проверить, что

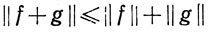
(f, g∈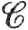(К)).

Значит, если определить расстояние между f и g как 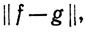то аксиома 2.17 для расстояния выполняется.

Используя эту метрику, мы можем определить теперь открытые множества, замкнутые множества, предельные точки, сходящиеся последовательности и т. д. в 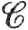(К). Расстояние в 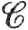(К) определено так, что последовательность {f_n} сходится к f тогда и только тогда, когда {f_n} сходится к f равномерно на К; {f_n} - последовательность Коши в 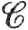(К) тогда и только тогда, когда {f_n} сходится равномерно на К. Значит, из теоремы 7.12 следует, что 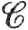(К) - полное метрическое пространство.

Замкнутые подмножества пространства 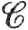(К) - это в точности те самые множества, которые в определении 7.26 были названы равномерно замкнутыми.

Всякое компактное подмножество в 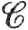(К) - это равномерно ограниченное равностепенно непрерывное множество функций. Обратно, замыкание каждого равномерно ограниченного равностепенно непрерывного множества функций из 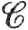(К) есть компактное подмножество пространства 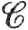(К). Это утверждение, по существу,- переформулировка теоремы 7.23.

Теорема 7.30 (теорема Стона - Вейерштрасса) может быть переформулирована так: если подалгебра в 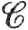(К), разделяющая точки множества К и не исчезающая ни в одной точке множества К, то алгебра плотна в пространстве (К).

Все эти замечания применимы также и к пространству всех комплексных функций, непрерывных на K; но только к условиям теоремы Стона-Вейерштрасса нужно добавить самосопряженность.