Равностепенно непрерывные семейства функций

В теореме 3.6 мы видели, что каждая ограниченная последовательность комплексных чисел содержит сходящуюся подпоследовательность. Возникает вопрос: верно ли что-либо подобное для последовательностей функций? Чтобы уточнить этот вопрос, мы определим два вида ограниченности.

7.19. Определение. Пусть {f_n} - последовательность функций, определенных на множестве Е.

Мы будем говорить, что последовательность {f_n} поточечно ограничена на Е, если последовательность {f_n(x)} ограничена при каждом х∈Е, т. е. если существует конечнозначная функция φ, определенная на Е и такая, что

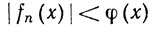
(x∈E, n = 1, 2, 3, ...).

Мы говорим, что последовательность {f_n} равномерно ограничена на множестве Е, если существует число М, такое, что

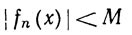
(x∈E, n = 1, 2, 3, ...).

Если последовательность {f_n} поточечно ограничена на множестве Е, а E₁ - счетное подмножество множества Е, то всегда можно найти подпоследовательность {f_nk}, такую, что последовательность {f_nk(х)} будет сходиться при каждом х∈Е₁. Это можно сделать с помощью диагонального процесса, который используется ниже при доказательстве теоремы 7.23.

Однако даже в том случае, когда {f_n} - равномерно ограниченная последовательность непрерывных функций на компактном множестве Е, не обязательно существует подпоследовательность, сходящаяся поточечно на Е. В приводимом ниже примере было бы затруднительно доказать это с помощью средств, которыми мы располагаем в настоящий момент, но доказательство оказывается совсем простым, если сослаться на теорему из гл. 10.

7.20. Пример. Пусть

Допустим, что существует строго возрастающая последовательность {n_k}, такая, что последовательность {sin n_kx} сходится при каждом х∈[0, 2π). В этом случае мы получим

(sin n_kx - sin n_k+1x) = 0 (0≤x≤2π).

значит,

(50)

(sin n_kx - sin n_k+1x)² = 0 (0≤x≤2π).

По теореме Лебега об интегрировании ограниченно сходящихся последовательностей (теорема 10.32), из (50) следовало бы, что

(51)

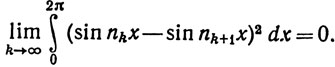
Однако простое вычисление дает

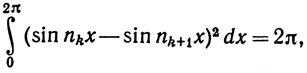
что противоречит равенству (51).

Другой вопрос таков: всякая ли сходящаяся последовательность содержит равномерно сходящуюся подпоследовательность? Следующий наш пример показывает, что это не обязательно имеет место даже в том случае, когда последовательность (непрерывных функций) определена на компактном множестве и равномерно ограничена на нем. (Пример 7.6 показывает, что последовательность ограниченных функций может быть сходящейся, не будучи равномерно ограниченной; но совершенно очевидно, что равномерная сходимость последовательности ограниченных функций влечет за собой их равномерную ограниченность.)

7.21. Пример. Пусть

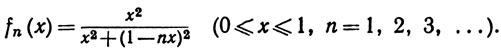
Тогда |f_n(х)|≤1, так что последовательность {f_n} равномерно ограничена на [0, 1]. Кроме того,

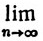f_n(x) = 0 (0≤x≤1).

но

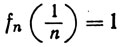
(n = 1, 2, 3, ...).

так что никакая подпоследовательность не сходится равномерно на [0, 1].

В этой связи нам понадобится понятие равностепенной непрерывности. Оно дано в следующем определении.

7.22. Определение. Семейство 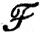функций f, определенных на подмножестве Е метрического пространства X, называется равностепенно непрерывным на Е, если для любого ε>0 существует δ>0, такое, что |f(x)-f(y)|<ε, когда d(x, y)<δ, x∈E, у∈Е, a f∈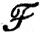. Здесь d обозначает расстояние в X.

Ясно, что каждая функция, входящая в состав равностепенно непрерывного семейства, равномерно непрерывна.

Последовательность {f_n} в примере 7.21 не является равностепенно непрерывной.

Равностепенная непрерывность и равномерная сходимость непрерывных функций тесно связаны друг с другом.

7.23. Теорема. Пусть К - компактное множество.

(b) Если {f_n} поточечно ограничена и равностепенно непрерывна на К, то {f_n} содержит равномерно сходящуюся подпоследовательность и равномерно ограничена на К.

Доказательство. Пусть ε>0, и пусхь выполнены предположения (а). Тогда существуют целое N и δ>0, такие, что

(52)

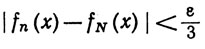
(x∈K, n>N)

и

(53)

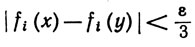
(1≤i≤N; d(x, y)&360;δ).

В (53) мы воспользовались тем фактом, что непрерывные функции равномерно непрерывны на компактных множествах. Если х∈К, у∈К, d(x, y)<δ и n>N, то

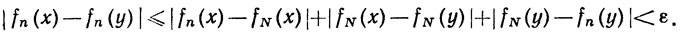
Последнее неравенство и неравенство (53) показывают, что утверждение (а) выполняется.

Докажем теперь утверждение (b). Не ограничивая общности, мы можем предположить, что компакт К содержит бесконечное число точек.

Сначала выберем в К счетное подмножество Е, такое, что Е плотно в К (т. е. такое, что К совпадает с замыканием множества Е).

Чтобы убедиться в существовании такого множества Е, можно рассуждать следующим образом. Пусть J(x, r) - множество всех точек у∈K, для которых d(х, у)<r. Из компактности множества К следует, что при каждом r>0 уже конечное число из них, скажем, J{х₁, r), ..., J(x_m, r) покрывают K. Полагая r = 1, ¹/₂, ¹/₃, ..., мы получаем счетную базу пространства К. (Определение базы см. в упражнении 11 к гл. 2.) Если выбрать по точке из каждого множества этой счетной базы, то полученное таким образом счетное множество окажется плотным в К.

Пусть {x_t}, t = 1, 2, 3, ..., - точки множества Е, расположенные в последовательность.

Ввиду того что последовательность {f_n(x₁)} ограничена, существует подпоследовательность, которую мы обозначим через {f₁

,k}, такая, что последовательность {f_1,k (x₁)} сходится при k→∞.

Рассмотрим теперь последовательности S₁, S₂, S₃, ..., которые можно расположить в таблицу

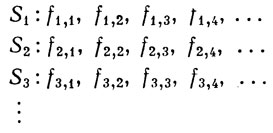
Пусть они обладают следующими свойствами:

(α) S_n - (бесконечная) подпоследовательность последовательности S_n-1 при n = 2, 3, 4, ... .

(β) {f_{n, k} (х_n)} сходится при k→∞ (ограниченность последовательности {f_n} позволяет выбрать S_n с таким свойством);

(γ) порядок, в котором выписываются функции, один и тот же во всех последовательностях, т. е. если одна из функций предшествует другой в S₁, то они так же расположены во всех S_n до тех пор, пока одна из этих функций не вычеркивается. Таким образом, передвигаясь из какой-нибудь строки таблицы в следующую строку вниз, функции могут переместиться влево, но никогда не перемещаются вправо.

Теперь мы спустимся по диагонали нашей таблицы, т. е. рассмотрим последовательность

(54)

Согласно (γ) последовательность S (за исключением, возможно, первых n-1 членов) - подпоследовательность последовательности S_n при n = 1, 2, 3, ... . Значит, из (β) следует, что последовательность {f_n,n(x_i)} сходится при n→∞ при каждом x_i∈E.

Пусть ε>0. Ввиду того что последовательность {f_n} равностепенно непрерывна, существует число δ>0, такое, что из d(х, у)<δ следует, что

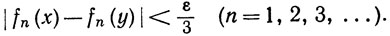
Пусть J(x, δ) имеет тот же смысл, что в начале доказательства. Существует конечный набор точек х₁, ..., х_р множества Е, такой, что

так как Е плотно в K, а К компактно. Выберем N так, чтобы иметь

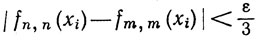
(i = 1, ..., p),

если n≥N, m≥N.

Тогда при любом х∈К существует точка x_i, такая, что 1≤i≤p и x∈J(x_i, δ); поэтому из n≥N, m≥N следует, что

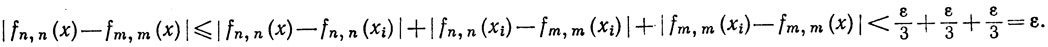
Таким образом, последовательность {f_{n, n}) сходится равномерно на К.

Чтобы доказать равномерную ограниченность последовательности {f_n} на множестве K, положим

(55)

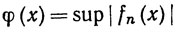
(n = 1, 2, 3, ...).

Задав ε>0, выберем δ>0 таким, чтобы из неравенства d(х, у)<δ следовало

(n = 1, 2, 3, ...).

Зафиксируем две точки х и у. Из неравенства

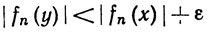
следует, что

(56)

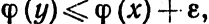
а из неравенства

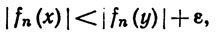
что

(57)

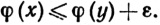
В силу (56) и (57),

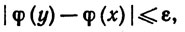
если только d(x, y)<δ, так что φ - функция, непрерывная на K. Функция φ ограничена, так как К - компактное множество. Теорема доказана.