
Равномерная сходимость и дифференцирование
Мы уже видели в примере 7.5, что из равномерной сходимости последовательности {fn} не следует даже поточечной сходимости последовательности {fn}. Таким образом, нужны более сильные предположения, чтобы заключить, что f'n→f' при fn→f.
7.17. Теорема. Пусть {fn} - последовательность дифференцируемых функций на [а, b], такая, что последовательность {fn(x0)} сходится при некотором х0∈[а, b]. Если последовательность {fn} сходится равномерно на [а, b], то и последовательность {fn} сходится равномерно на [а, b] к некоторой функции f, причем
(37) f'(x) = 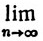 f'n(x) (a≤x≤b).
f'n(x) (a≤x≤b).
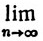 f'n(x) (a≤x≤b).
f'n(x) (a≤x≤b).Доказательство. Пусть ε&362;0. Выберем такое N, что из n≥N, m≥N следует
(38)
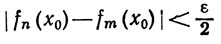
и
(39)
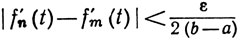
(a≤t≤b).
Если мы применим теорему 5.20 о среднем значении к функции fn-fm, то, как показывает (39), мы получим
(40)
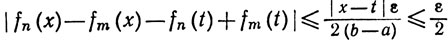
при любых х и t из [а, b] для n≥N, m≥N. Из неравенства
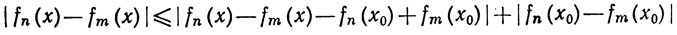
следует, в силу (38) и (40), что
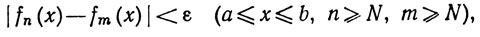
а потому {fn} сходится равномерно на [a, b]. Пусть f(x) =  fn(x) (a≤x≤b).
fn(x) (a≤x≤b).
Зафиксируем точку х сегмента [a, b] и положим
(41)
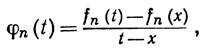
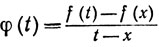
при a≤t≤b, t≠x. Тогда
(42)
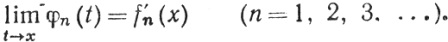
Первое неравенство в (40) показывает, что
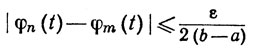
(n≥N, m≥N),
поэтому {φn} сходится равномерно при t≠x. Поскольку {fn} сходится к f, то, в силу (41),
(43)
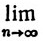 φn(t) = φ(t)
φn(t) = φ(t)равномерно на множестве всех t, таких, что а≤t≤b, t≠x.
Применяя к последовательности {φn} теорему 7.11, заключаем на основании (42) и (43), что
а это, в силу определения функции φ(t), и есть (37).
Замечание. Если дополнительно предположить, что функции f'n непрерывны, то можно получить гораздо более короткое доказательство равенства (37), опирающееся на теорему 7.14 и на основную теорему интегрального исчисления.
7.18. Теорема. Существует вещественная непрерывная на вещественной прямой функция, которая нигде не дифференцируема.
Доказательство. Положим
(44)
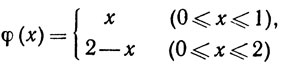
и доопределим φ(х) для всех остальных вещественных х, полагая
φ(х + 2) = φ(х).
Тогда функция φ непрерывна на R1. Пусть
(45)
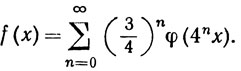
Поскольку 0≤φ≤1, то, как показывает теорема 7.10, ряд (45) сходится равномерно на R1, так что функция f непрерывна на R1 по теореме 7.12.
Зафиксируем теперь вещественное число х и положительное целое m. Существует целое k, такое, что
(46)
k≤4mx&38804;k+1.
Положим
(47)
αm = 4-mk, βm = 4-m(k+1).
и рассмотрим числа 4nβm и 4nαm. Если n>m, то их разность - четное целое; если n = m, то они целые, а их разность равна 1; если n<m, то между ними не лежит ни одно целое число. Значит,
(48)
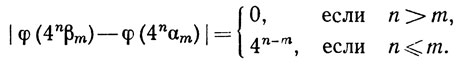
Согласно (45) и (48),
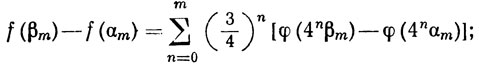
следовательно,
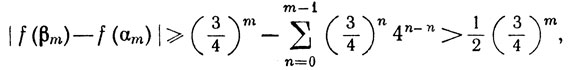
или
(49)
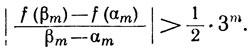
Теорема 5.19 и неравенство (49) показывают, что функция f не дифференцируема в точке х, так как αm≤x≤βm и βm-αm→0 при m→∞.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'