Равномерная сходимость и интегрирование

7.14. Теорема. Пусть α - монотонно возрастающая на [а, b] функция. Пусть fn∈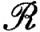(α) на [а, b] при n = 1, 2, 3, ..., и пусть f_n→f равномерно на [а, b]. Тогда f#8712;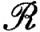(α) на [а, b] и

(26)

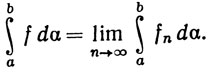
(Существование предела в (26) заранее не предполагается.)

Доказательство. Достаточно доказать теорему для вещественных f_n. Пусть задано ε>0. Выберем η>0 так, что

(27)

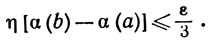
Существует такое целое n, что

(28)

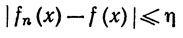
(a≤x≤b),

так как сходимость равномерна.

Зафиксируем n и выберем разбиение Р сегмента [а, b] так, чтобы иметь

(29)

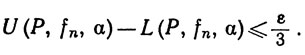
Это возможно по теореме 6.6.

Поскольку f(x)≤f_n(х) + η, из (27) далее вытекает, что

(30)

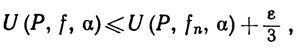
а так как f(x)≥f_n(х) - η, то

(31)

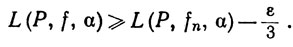
Комбинируя (29), (30) и (31), получаем

(32)

откуда следует, что f∈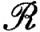(α) на [a, b] (по теореме 6.6).

Для доказательства равенства (26) выберем такое N, что из n≥N следует

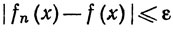
Тогда при n≥N

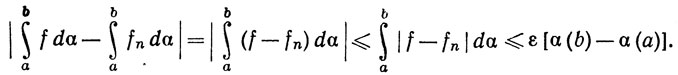
Поскольку ε>0 произвольно, отсюда вытекает (26).

Следствие.Если f∈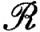(α) на [a, b] и если

f(x) 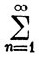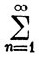= f_n(x) (a≤x≤b),

причем ряд сходится равномерно на [a, b], то

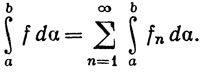
Иными словами, ряд можно интегрировать почленно.

При изучении последовательностей интегралов вида

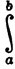fdg_n ( n = 1, 2 ,3, ...),

где функция f непрерывна, а функции g_n - ограниченной вариации на [а, b], обнаруживается, что равномерная сходимость последовательности {g_n} к g - условие, еще недостаточно сильное, чтобы обеспечить равенство

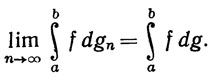
7.15. Пример. Пусть

(33)

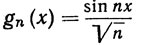
(0≤x≤2π, n = 1, 2, 3, ...)

и

(34)

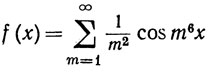
(0≤x≤2π).

По теореме 7.10 ряд в (34) сходится равномерно, так что функция f непрерывна на [0, 2π]. Кроме того, g_n→0 равномерно на [0, 2π]. Теперь заметим, что

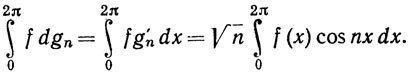
Положим n = р⁶, где р - положительное целое. Ряд (34), почленно умноженный на cosnx, также сходится равномерно, и мы можем проинтегрировать его почленно. Поскольку

cos nx* cos mx dx = 0,

каковы бы ни были различные положительные числа m, n, имеем

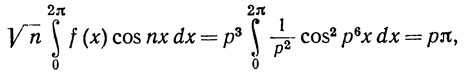
так что при n = р⁶

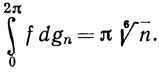
Таким образом, числа f dg_n образуют неограниченную последовательность, хотя g_n→0 равномерно.

Теперь мы сформулируем имеющийся здесь положительный результат.

7.16. Теорема. Пусть {g_n} - последовательность функций ограниченной вариации на [а, b], причем g_n(a) = 0, и пусть g - такая функция, что

(35)

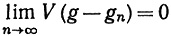
и g(a) = 0. Тогда для любой функции f, непрерывной на [a, b], имеем

(36)

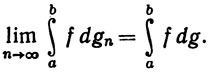
Кроме того, g_n→g равномерно на [а, b].

Здесь V, как обычно, обозначает полную вариацию на [а, b].

Доказательство. Вследствие неравенства

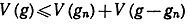
(теорема 6.24) g - функция ограниченной вариации на [а, b], так что все интегралы в (36) существуют. Пусть |f(x)|≤M на [а, b]. Тогда

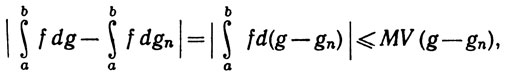
и (36) следует из (35).

Кроме того, g_n→g равномерно, так как

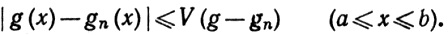
Заметим, что предположение g_n(a) = g(а) = 0 сделано только ради удобства. Прибавив постоянные с_n к функциям g_n, мы не изменим интегралов, а сходимость последовательности {g_n(x)} для одного значения х∈[а, b], как легко показать, влечет за собой равномерную сходимость.

За другими относящимися сюда результатами мы отсылаем к упражнениям 9 и 10.