Равномерная сходимость и непрерывность

7.11. Теорема. Пусть f_n→f равномерно на подмножестве Е некоторого метрического пространства. Пусть х - предельная точка множества Е, и пусть

(15)

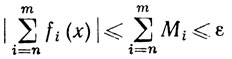
(n = 1, 2, 3, ...).

Тогда последовательность {A_n} сходится и

(16)

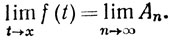
Иными словами, в данном случае

(17)

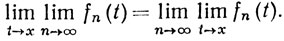
Доказательство. Пусть ε>0. В силу равномерной сходимости последовательности {f_n}, существует такое N, что из n≥N, m≥N, t∈E следует неравенство

(18)

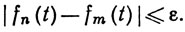
Полагая в (18) t→x, получаем

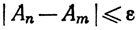
при n≥N, m≥N, так что {А_n} - последовательность Коши, и потому сходится. Обозначим ее предел через А.

Далее,

(19)

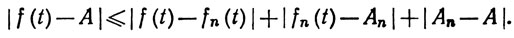
Выберем сначала n так, что

(20)

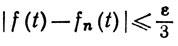
при всех t∈E (это возможно в силу равномерной сходимости) и что

(21)

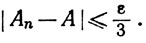
Затем для этого n мы подберем такую окрестность V точки х, что из t∈V, t≠x следует

(22)

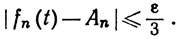
Подставляя неравенства (20), (21) и (22) в (19), мы получим

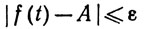
для всех t∈V, t≠x. Но это равносильно равенству (16).

7.12. Теорема. Если {f_n} - последовательность функций, непрерывных на множестве Е, и если f_n→f равномерно на Е, то и функция f непрерывна на множестве Е.

Этот очень важный результат сразу следует из теоремы 7.11.

Обратное неверно, т. е. последовательность непрерывных функций может неравномерно сходиться к непрерывной функции. Соответствующий пример дает последовательность (10) из п. 7.6 (для того чтобы убедиться в том, что эта последовательность сходится неравномерно, достаточно применить теорему 7.9). Тем не менее в некоторых случаях можно утверждать обратное. В частности, имеет место следующая теорема.

7.13. Теорема. Пусть множество Е компактно. Пусть {f_n} - последовательность функций, непрерывных на Е, сходящаяся к непрерывной функции f на Е. Если f_n(x)≥f_n+1(x) при n = 1, 2, 3, ... и при любом х∈Е, то f_n→f равномерно на Е.

Доказательство. Положим g_n(x) = f_n(x) - f(x). Тогда g_n - непрерывная функция, g_n→0 и g_n≥g_n+1. Мы должны доказать, что g_n→0 равномерно на Е.

Пусть ε>0. При любом х∈Е существует целое число n_х, такое, что

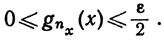
В силу непрерывности функций g_n и монотонности последовательности {g_n} существует открытое множество J(x), содержащее точку х и такое, что

(23)

если t∈J(x) и n≥n_х.

Поскольку Е - компактное множество, существует конечное множество точек х₁, ..., х_m, таких, что

(24)

Полагая

на основании (23) и (24) мы заключаем, что

при всех t∈Е, если n≥N. Тем самым доказано, что сходимость равномерна.

Отметим, что компактность здесь существенна. Например, если

(25)

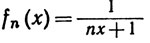
(0<x<1, n = 1, 2, 3, ...),

то f_n(х)→0 монотонно на (0, 1), но сходимость неравномерна.