Равномерная сходимость

7.7. Определение. Мы будем говорить, что последовательность функций {f_n}, n = 1, 2, 3, ..., сходится равномерно на множестве Е к функции f, если для любого ε>0 существует целое число N, такое, что при n≥N имеем

(12)

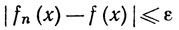
для всех х∈Е.

Ясно, что каждая равномерно сходящаяся последовательность сходится и поточечно. Разница между этими двумя понятиями заключается в следующем. Если последовательность {f_n} сходится поточечно на Е, то существует функция f, такая, что для любого ε>0 и для любого х∈Е существует целое число N, зависящее от ε и от х, такое, что (12) выполняется при n≥N; если же {f_n} сходится равномерно на Е, то можно при каждом ε>0 найти одно целое число N, которое будет годиться при всех х∈Е.

Мы будем говорить, что ряд ∑f_n(x) сходится равномерно на множестве Е, если последовательность {s_n} частных сумм, определенных равенством

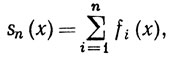
равномерно сходится на множестве Е.

Следующая теорема представляет собой критерий Коши равномерной сходимости.

7.8. Теорема. Последовательность функций {f_n}, определенных на Е, сходится равномерно на Е тогда и только тогда, когда для любого ε>0 существует целое N, такое, что при m≥N, n≥N, x∈E имеем

(13)

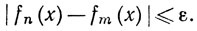
Доказательство. Допустим, что {f_n} сходится равномерно на Е, и пусть f - предельная функция. Тогда существует целое число N, такое, что из n≥N, x∈E следует неравенство

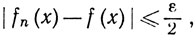
так что

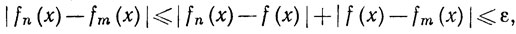
если n≥N, m≥N, х∈Е.

Обратно, пусть выполняется условие Коши. По теореме 3.11 последовательность {f_n(x)} сходится при каждом х к пределу, который мы обозначим через f(х). Мы должны доказать, что сходимость равномерна.

Пусть задано число ε>0. Выберем N так, чтобы выполнялось (13). Зафиксируем n и устремим m к ∞ в (13). Ввиду того что f_m(х)→f(х) при тm→∞, получаем

(14)

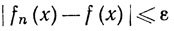
при любом n≥N и любом х∈Е. Доказательство закончено.

Иногда полезен следующий критерий.

7.9. Теорема. Пусть

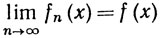
(x∈E).

Положим

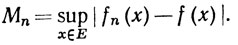
Тогда f_n→f равномерно на Е в том и только в том случае, когда М_n→0 при n→∞.

Мы не приводим подробного доказательства, так как это утверждение непосредственно следует из определения 7.7.

Вейерштрассу принадлежит очень удобный признак равномерной сходимости рядов.

7.10. Теорема. Пусть {f_n} - последовательность функций, определенных на множестве Е, и пусть

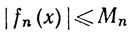
(x∈E, n = 1, 2, 3, ...).

Тогда ряд ∑f_n сходится равномерно на Е, если ряд ∑М_n сходится.

Заметим, что обратное не утверждается (и в действительности неверно).

Доказательство. Если ряд ∑М_n сходится, то при любом ε>0

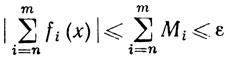
если только m и n достаточно велики. Равномерная сходимость вытекает теперь из теоремы 7.8.