Вводные замечания

7.1. Определение. Пусть {f_n}, n = 1, 2, 3, ... - последовательность функций, определенных на множестве Е, и пусть последовательность чисел {f_n(x)} сходится при каждом х∈Е. Тогда мы можем определить функцию f, полагая

(1)

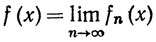
(x∈E).

В подобных случаях мы будем говорить, что последовательность {f_n} сходится на множестве Е и что f - предел, или предельная функция, последовательности {f_n}. Иногда мы будем говорить, что последовательность {f_n} сходится к функции f поточечно на множестве Е, если выполнено условие (1). Аналогично, если ряд ∑ f_n(х) сходится при любом х∈Е, то мы полагаем, по определению,

(2)

(x∈E).

причем функция f называется суммой ряда ∑f_n.

Главная из возникающих в связи с этими определениями проблем такова: выяснить, сохраняются ли важнейшие свойства функций при выполнении предельных операций (1) и (2). Например, если функции f_n непрерывны, или дифференцируемы, или интегрируемы, то верно ли то же самое в отношении предельной функции? Каковы соотношения между, скажем, f'_n и f' или между интегралами от f_n и от f?

Непрерывность функции f в точке х означает, что

Значит, спросить, будет ли предел последовательности непрерывных функций непрерывной функцией, это все равно, что спросить, верно ли равенство

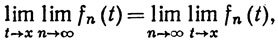
т. е. важен ли порядок, в котором осуществляются предельные переходы. В левой части равенства (3) мы сначала устремляем n к ∞ , затем t к х; в правой части -сначала t→x, а затем n→∞ .

Мы покажем сейчас на примерах, что, вообще говоря, два предельных перехода нельзя переставить без того, чтобы это не повлияло на результат. Затем мы докажем, что при некоторых условиях порядок, в котором выполняются операции предельного перехода, не имеет значения.

Наш первый и простейший пример связан с "двойной последовательностью".

7.2. Пример. Для m = 1, 2, 3, ..., n = 1, 2,3, ... положим

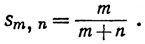
Тогда при каждом фиксированном n

так что

(4)

С другой стороны, при каждом фиксированном m

так что

(5)

7.3. Пример. Пусть

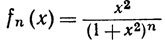
(х вещественно, n = 0, 1, 2, ...),

и пусть

(6)

Так как f_n(0) = 0, то и f(0) = 0. Ряд (6) представляет сумму геометрической прогрессии, и при х≠0 эта сумма равна 1+x². Значит,

так что сходящийся ряд, составленный из непрерывных функций, может иметь разрывную сумму.

7.4. Пример. При m = 1, 2, 3, ... положим

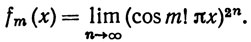
Если m! x - целое число, то f_m(x) = 1. Для всех остальных значений х имеем f_m(x) = 0. Теперь положим

Если х - иррациональное число, то f_m(x) = 0 при всех m, значит, f(x) = 0. Если x - рациональное число, скажем, x = ^p/_q, то при m≥q произведение m! х - целое число, так что f(x) = 1. Значит,

Таким образом, мы получили всюду разрывную предельную функцию, которая не интегрируема по Риману (упражнение 7, гл. 6).

7.5. Пример. Пусть

(9)

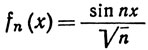
(x вещественно, n = 1, 2, 3, ...)

и

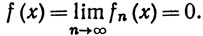
Тогда f'(x) = 0, но

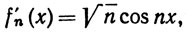
так что {f'_n} не сходится к f'. Например,

при n→∞, тогда как f'(0) = 0.

7.6. Пример. Пусть

(10)

Если 0⊾х≤1, то

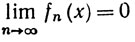
по теореме 3.20 (d). Ввиду того что f_n(0) = 0 при всяком n,

(11)

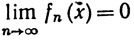
(0≤x≤1).

Простое вычисление показывает, что

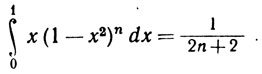
Таким образом, несмотря на (11),

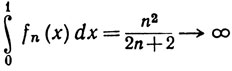
Если в (10) заменить коэффициент n² на n, то (11) все еще выполняется, но теперь

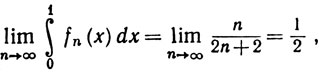
тогда как

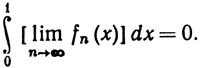
Таким образом, предел интеграла не обязан совпадать с интегралом от предела даже тогда, когда оба эти предела конечны.

После этих примеров, показывающих, что беззаботная перестановка порядка предельных переходов может привести к ошибке, мы определим новый вид сходимости, более сильный, чем поточечная сходимость, описанная в определении 7.1. Этот новый вид сходимости позволит нам прийти к положительным результатам.