Упражнения

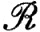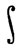1. Пусть функция α возрастает на [а, b], а≤x₀≤b, α непрерывна в точке х₀, f(x₀) = 1 и f(х) = 0, если х≠х₀. Доказать, что f∈(α) и fdα = 0.

2. Пусть f≥0, непрерывна на [а, b] и 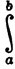f(x) dx = 0. Доказать, что f(x) = 0 при всех x∈[a, b] (ср. с упражнением 1).

3. Определим три функции β₁, β₂, β₃ следующим образом: β_j(х) = 0, если x<0, β_j(x) = 1, если х>0 при j = 1, 2, 3; β₁(0) = 0, β₂(0) = 1, β₃(0) = ¹/₂. Пусть f - ограниченная функция на [-1, 1].

(а) Доказать, что f∈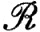(β₁) тогда и только тогда, когда f (0+) = f(0), и что в этом случае

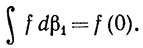
(b) Сформулировать и доказать аналогичный результат для β₂.

(c) Доказать, что f∈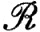(β₃) тогда и только тогда, когда f непрерывна в точке 0.

(d) Пусть f непрерывна в точке 0. Доказать, что

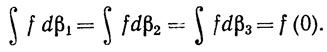
4. Используя обозначения упражнения 3, доказать, что β₂∈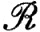(β₁), несмотря на то что lim S(P, β₂, β₁) при μ(P)→0 не существует.

5. Пусть {х_n} - последовательность различных точек интервала (0, 1), и пусть c_n>0, ∑ c_n<+ ∞. Положим

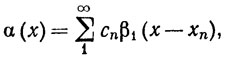
где функция β₁ определена так же, как в упражнении 3. Пусть f непрерывна на (0, 1). Доказать, что

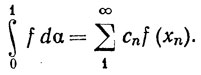
Указание. Положим 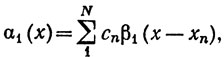α₂ = α-α₁. Согласно упражнению 3, 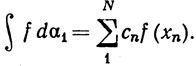Кроме того, 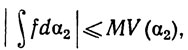где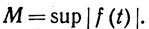

6. Пусть f отображает сегмент [а, b] в пространство R^k, причем f - функция ограниченной вариации. Доказать, что функция v_f непрерывна в точке х∈[а, b] тогда и только тогда, когда функция f непрерывна в этой точке.

7. Пусть f(x) = 0 при всех иррациональных х, f(х) = 1 при всех рациональных х. Доказать, что f∉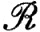 на [а, b] при любых а, b, таких, что а<b.

8. Показать, что

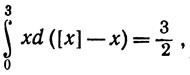
где [x] - наибольшее из целых чисел, не превосходящих х (см. определение в упражнении 2 гл. 4).

9. Вычислить функции положительной, отрицательной и полной вариации функций

(a) f(x) = 3x²-2x³ (-2≤x≤2),

(b) f(x) = [x]-x (0≤x≤2).

10. Пусть f - вещественная функция ограниченной вариации на [a, b], р и q - функции положительной и отрицательной вариации функции f, p₁ и q₁ - возрастающие функции на [a, b] и f = p₁-q₁. Тогда V(p)≤V(p₁) и V(q)≤V(q₁), где V обозначает полную вариацию на [а, b].

11. Пусть g∈ на [а, b]. Положим

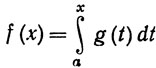
и g⁺(t) = max (g(t), 0), g^-(t)= - min(g(t), 0). Доказать, что f - функция ограниченной вариации на [а, b] и что ее функции вариации задаются равенствами

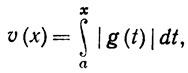
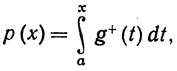
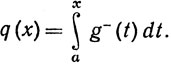
12. Пусть f - функция ограниченной вариации на сегменте (0, 2π] и f(2π) = f(0). Доказать, что каждый из интегралов

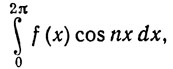
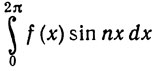
нe превосходит ^V(f)/_n по абсолютной величине.

Указание. Проверить, что

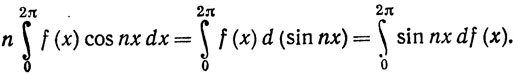
13. Пусть γ₁, γ₂, γ₃ - кривые в комплексной плоскости, определенные на [0, 2π) равенствами

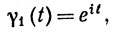
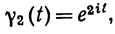
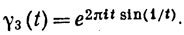
Показать, что эти три кривые имеют одно и то же множество значений, что γ₁ и γ₂ спрямляемы, что длина кривой γ₁ равна 2π, длина кривой γ₂ равна 4π, а кривая γ₃ не спрямляема.

14. Пусть γ₁ - кривая в R^k, заданная на [а, b]; пусть φ - непрерывное взаимно однозначное отображение сегмента [с, d] на сегмент [а, b], такое, что φ(с) = а. Положим, по определению, γ₂(s) = γ₁(φ(s)). Доказать, что дуга γ₂ - простая замкнутая спрямляемая кривая тогда и только тогда, когда то же самое верно в отношении γ₁. Доказать, что γ₂ и γ₁ имеют одну и ту же длину.

15. Пусть α возрастает на [а, b], f и g - комплексные функции, причем f∈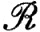(α), g∈(α) на [а, b]. Доказать неравенство Шварца

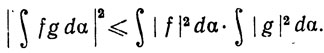
Указание. Следовать доказательству теоремы 1.62. Вывести аналогичный результат, предполагая только, что α - функция ограниченной вариации.

16. Если f∈ [a, b] для любого b>а и фиксированного α, то положим

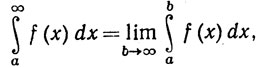
если этот предел существует; в этом случае мы будем говорить, что интеграл сходится.

Доказать так называемый "интегральный признак" сходимости рядов: если f(x)≥0 и f монотонно убывает при x≥1, то

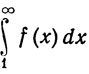
сходится в том и только в том случае, когда сходится ряд

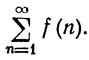
17. Пусть функции f и g непрерывны на [а, b] и α - функция ограниченной вариации на [а, b]. Положим

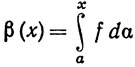
Доказать, что

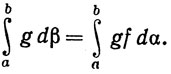
(a≤x≤b).

18. Если γ - спрямляемая кривая в комплексной плоскости, заданная на [0, 1], и если f - комплексная непрерывная функция, заданная на множестве значений кривой γ, то положим, по определению,

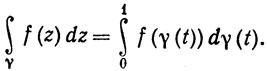
Пусть γ(0) = A, γ(1) = В. Доказать, что

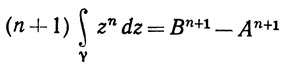
(n = 0, 1, 2, 3, ...).

Указание. Рассмотреть случай A = 0. При n = 0 результат тривиален. Допустим, что он верен при некотором n. Положим f = γⁿ, g = γ, α = γ и определим β, как в упражнении 17. По предположению индукции,

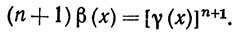
Применить упражнение 17 и проинтегрировать по частям.

19. Положим

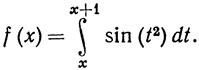
(a) Доказать, что 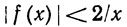при х>0.

Указание. Положить t² = u и воспользоваться второй теоремой о среднем значении.

(b) Найти верхний и нижний пределы функции xf(x) при х→ ∞.