Спрямляемые кривые

В заключение этой главы мы рассмотрим одно интересное геометрическое приложение некоторой части предшествующей теории. Случай k = 2 (т. е. случай плоских кривых) особенно важен при изучении аналитических функций комплексной переменной.

6.34. Определение. Непрерывное отображение у сегмента [a, b] в пространство R^k называется кривой в R^k. Если отображение γ взаимно однозначно, то γ называется дугой. Если γ(а) = γ(b), но γ(t₁)≠γ(t₂). Для любой другой пары различных точек t₁, t₂, принадлежащих сегменту [а, b], то γ называется простой замкнутой кривой.

Следует заметить, что кривая определяется как отображение, а не как множество точек. Конечно, с каждой кривой в R^k связано некоторое множество точек в R^k, а именно множество значений отображения γ однако для разных кривых это множество может оказаться одним и тем же.

Мы будем называть кривую γ спрямляемой, если γ - функция ограниченной вариации; длиной кривой γ мы будем называть число V (γ; а, b).

Чтобы обосновать это определение, напомним, что V (γ; а, b) - это верхняя грань множества всех сумм вида

(56)

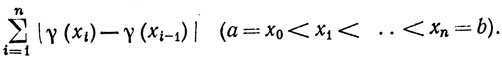
В этой сумме i-е слагаемое равно расстоянию (в R^k) между точками γ(x_i-1) и γ(x_i) а сама сумма равна длине ломаной с вершинами в точках γ(х₀), γ(х₁), ..., γ(х_n), расположенных в указанном порядке. Когда диаметр разбиения стремится к нулю, эти ломаные приближаются к множеству значений отображения γ. Разумеется, мы здесь ничего не доказываем, а лишь пытаемся объяснить разумность такого определения длины.

В некоторых случаях длина кривой выражается интегралом Римана. Мы докажем это для непрерывно дифференцируемых кривых, т. е. для кривых γ, производная γ' которых непрерывна.

6.35. Теорема. Если функция γ' непрерывна на [а, b], то γ спрямляема, а ее длина равна

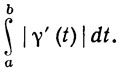
Доказательство. Мы должны доказать, что |γ'| = V(γ)

Если {x₀, ..., х_n) - разбиение сегмента [а, b], то, как показывают теоремы 6.19 и 6.20,

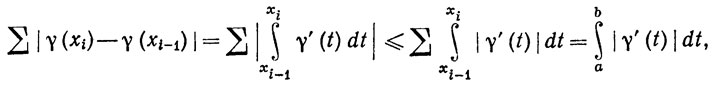
так что

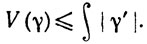
Пусть ε>0. Ввиду того что функция γ' равномерно непрерывна на [а, b], существует δ>0, такое, что |γ'(s)-γ'(t)|<ε, если |s - t|<δ. Пусть {х₀, ..., х_n} - разбиение сегмента [а, b], диаметр которого меньше δ. Если x_i-1≤t≤x_i, то

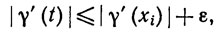
так что

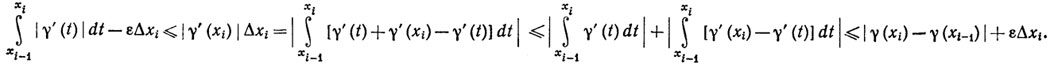
Суммируя эти неравенства по i = 1, ..., n, мы получим

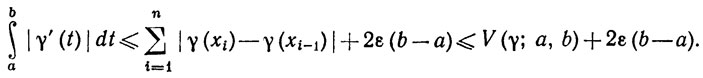
Ввиду произвольности ε отсюда следует, что 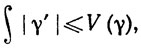и доказательство закончено.