
Дальнейшие теоремы об интегрировании
6.28. Определение. Теперь мы обратимся к интегрированию относительно любой функции ограниченной вариации, а не только относительно монотонной функции. Если α - вещественная функция ограниченной вариации на [а, b] и если α = β-γ, где β и γ - возрастающие функции, то естественное определение таково:
(47)
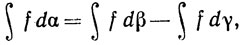
если только оба интеграла справа существуют в том смысле, в каком они были определены ранее.
Если α = β1-γ1 - другое разложение функции а в разность возрастающих функций, то β+γ1 = β1+γ, и поэтому [см. теорему 6.10 (е)]
(48)
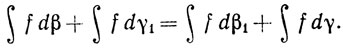
Отсюда следует, что интеграл 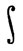 fdα, определенный в (47), не зависит от выбора разложения функции α, если только f принадлежит множествам
fdα, определенный в (47), не зависит от выбора разложения функции α, если только f принадлежит множествам 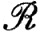 (β)
(β) 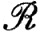 (β1),
(β1), 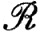 (γ) и
(γ) и 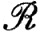 (γ1).
(γ1).
Поэтому в дальнейшем в этой главе мы будем рассматривать лишь два случая, когда все интересующие нас интегралы автоматически существуют:
(a) функция f непрерывна, функция α - ограниченной вариации;
(b) функции f и α - ограниченной вариации и α непрерывна.
В случае (а) мы сошлемся на теорему 6.8. В случае (b) условимся представлять α в виде разности только непрерывных монотонных функций [это можно сделать, согласно следствию 1 из теоремы 6.27]; разлагая f в разность монотонных функций, мы сошлемся на теорему 6.9.
Заметим, кроме того, что в обоих случаях теорема 6.14 применима в полном объеме.
Теперь мы могли бы, конечно, распространить это определение на векторнозначные функции f. Однако более интересным представляется другое обобщение, которое применяется в теории аналитических функций. Это обобщение получится, если обе функции f и α считать комплексиозначными.
Если f = f1+if2, α = α1+iα2, где f1, f2, α1, α2 - вещественные функции на [a, b], и если выполняется условие (а) или (b), то мы положим
(49)
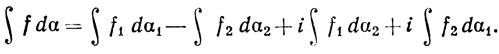
Четыре интеграла, стоящие в правой части этого равенства, были определены в (47).
Обычные свойства аддитивности [теоремы 6.10 (а), (с), (е)] в этой ситуации легко проверяются. Рассмотрим теперь аналог теоремы 6.12 (b) [см. также теорему 6.20] для комплексных α.
6.29. Теорема. Пусть f и α - комплексные функции на [а, b], удовлетворяющие условиям (а) или (b) определения 6.28. Пусть v - функция полной вариации функции α на [а, b]. Тогда
(50)
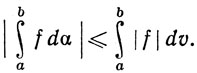
Следствие.
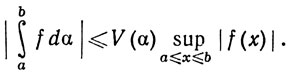
Доказательство. Если выполнено (а), то функция |f| непрерывна. Если выполнено (b), то непрерывна функция v (теорема 6.26), а так как f - функция ограниченной вариации, то такова и функция |f|. Значит, второй интеграл в (50) существует в обоих случаях.
Для любого разбиения Р = {х0, x1, ..., хn} сегмента [a, b] имеем
(51)
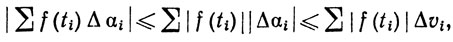
если xi-1≤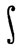 fdα, а последняя - к
fdα, а последняя - к 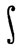 |f|dv по теореме 6.14. Тем самым неравенство (50) доказано.
|f|dv по теореме 6.14. Тем самым неравенство (50) доказано.
6.30. Теорема. Пусть f и α - комплексные функции ограниченной вариации на [а, b], а функция f, кроме того, непрерывна. Тогда
(52)
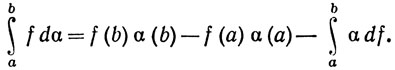
Замечание. По аналогии с приемом суммирования по частям равенство (52) называют формулой интегрирования по частям. Часто оказывается удобным рассматривать 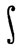 αdf вместо
αdf вместо 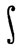 fdα.
fdα.
Доказательство. Выберем какое-нибудь разбиение Р = = {х0, х1, ...,хn) сегмента [а, b]. Выберем t1, ..., tn так, что xi-1≤ti≤xi, положим t0 = a, tn+1 = b, и пусть Q - разбиение {t0, t1, ..., tn+1} сегмента [а, b]. Тогда, суммируя по частям, получим
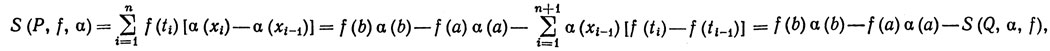
так как ti-1≤xi-1≤ti. Если μ(P)→0, то и μ(Q)→0, и теорема 6.14 показывает, что S(P, f, α)→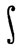 fdα, S(Q, α, f)→
fdα, S(Q, α, f)→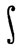 αdf. Отсюда следует равенство (52).
αdf. Отсюда следует равенство (52).
Замечание. Если функция f непрерывна, а α-функция ограниченной вариации, то (52) можно использовать для определения интеграла 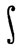 αdf даже в том случае, когда f не есть функция ограниченной вариации. Это приводит еще к одному обобщению стильтьесовского процесса интегрирования, которое мы, однако, не будем в дальнейшем рассматривать.
αdf даже в том случае, когда f не есть функция ограниченной вариации. Это приводит еще к одному обобщению стильтьесовского процесса интегрирования, которое мы, однако, не будем в дальнейшем рассматривать.
В следующих двух теоремах мы должны будем ограничиться вещественными функциями - так же, как и в случае теорем о среднем в теории дифференцирования.
6.31. Теорема. (Первая теорема о среднем значении.) Если f непрерывна и вещественна, а α монотонно возрастает на [а, b], то существует точка х, такая, что а≤x≤b и
(53)
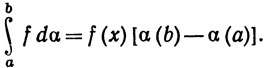
Доказательство. Положим
M = sup f(t), m = inf f(t) (a≤t≤b).
Тогда
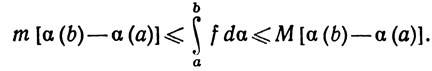
Значит, существует число λ, такое, что m≤λ≤M и
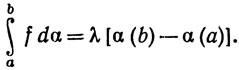
В силу теорем 4.16 и 4.23 существует точка х, принадлежащая сегменту [а, b], для которой f(x) = λ, откуда и следует (53).
Замечание. Может случиться, что точку х нельзя выбрать так, что a<x<b. Например, если
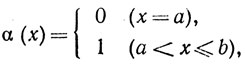
a f непрерывна, то ь
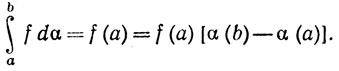
6.32. Теорема. (Вторая теорема о среднем значении.) Пусть функция f монотонна, а α - функция ограниченной вариации, вещественная и непрерывная на [а, b]. Тогда существует такая тонка х∈[а, b], что
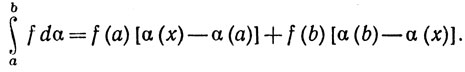
Доказательство. Согласно теоремам 6.30 и 6.31,
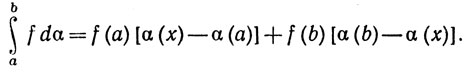
при некотором х∈[а, b].
6.33. Теорема. (Замена переменной.) Пусть f и φ непрерывны на [а, b], φ строго возрастает на [а, b], а ψ-функция, обратная к φ. Тогда
(54)
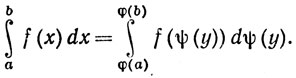
[Формально (54) получается, если положить у = φ(х), х = ψ(у).]
Доказательство. Для любого разбиения Р
a = x0≤x1≤x2≤...≤xn-1≤xn = b
положим уi = φ(хi) (i = 0,...,n) и рассмотрим разбиение Q:
φ(a) = y0≤y1≤...≤yn-1≤yn≤ = φ(b).
Полагая g(y) = f(ψ(y)), получаем
(55)
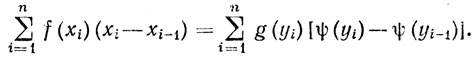
В силу равномерной непрерывности функции ф на [а, b] (теорема 4.19), если μ(Р)→0, то μ(Q)→0. Таким образом, если μ(Р)→0, то обе части равенства (55) стремятся к соответствующим частям равенства (54), поскольку функция g непрерывна. Доказательство закончено.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'