Функции ограниченной вариации

До сих пор мы занимались интегрированием относительно монотонных функций α. В самом деле, неравенство Δα_i≥0 играло основную роль во всех доказательствах, связанных с L(P, f, α) и U(P, f, α). Рамки теории интегрирования, развитой в предыдущих разделах, можно расширить без значительных трудностей, если заменить класс монотонных функций классом функций ограниченной вариации. Чтобы избежать повторений, мы сразу же определим этот класс для векторнозначных функций.

6.21. Определение. Пусть f - отображение сегмента [а, b] в пространство R^k. Если Р = {х₀, ..., х_n) - разбиение сегмента [а, b], то положим

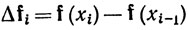
и

(37)

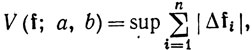
где верхняя грань берется по всем разбиениям сегмента [а, b].

Назовем число V (f; a, b) полной вариацией отображения f на сегменте [а, b]. Если из контекста ясно, о каком сегменте идет речь, то мы будем сокращенно писать V(f).

Если V(f; а, b)<+∞, то говорят, что f - функция ограниченной вариации на [а, b].

Многие свойства векторнозначных функций ограниченной вариации можно получить сведением к случаю вещественных функций.

6.22. Теорема. Пусть f = (f₁, ..., f_k) отображает сегмент [а, b] в пространство R^k. Тогда f - функция ограниченной вариации на [а, b] в том и только в том случае, когда каждая из функций f_j имеет ограниченную вариацию на [а, b]. Для 1≤j≤k имеем

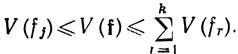
Доказательство. Для любого разбиения {х₀, ..., х_n) сегмента [а, b] имеем

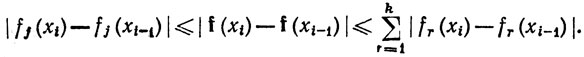
Если мы просуммируем эти неравенства по i = 1, ..., n, а затем перейдем к верхним граням, то мы получим утверждение теоремы.

6.23. Примеры.(а) Если f - монотонная функция на [а, b], то f - функция ограниченной вариации на [а, b], и V(f) = |f(b)-f(a)|.

(b) Если f' существует и ограничена на [а, b], то f - функция ограниченной вариации. Действительно, если |f'(х)|≤М, то по теореме 5.20

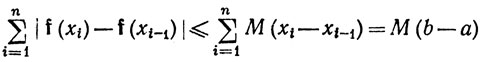
для любого разбиения сегмента [а, b].

(c) Функция f может быть непрерывной, не будучи функцией ограниченной вариации. Рассмотрим функцию

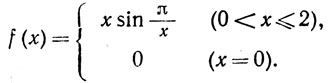
Выберем разбиение, состоящее из точек

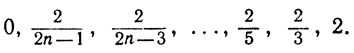
Соответствующая сумма, фигурирующая в (37), равна в этом случае

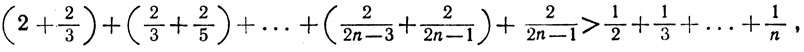
а это число может быть сделано сколь угодно большим за счет выбора достаточно большого n, ибо ряд ∑¹/_n - расходится.

(d) Ясно, что каждая функция ограниченной вариации ограничена, так как |f(x) - f(a)|&$8804;V(f) при всех х∈[а, b].

Мы увидим (теорема 6.27), что существует тесная связь между функциями ограниченной вариации и монотонными функциями. Сумма или произведение двух монотонных функций не обязательно монотонны. Например, х и х² монотонны на [0, 1], а функция х-х² не монотонна; функция х монотонна на [-1, 1], а функция х² - нет. Однако класс функций ограниченной вариации замкнут относительно операций сложения и умножения.

6.24. Теорема. Если f и g - комплексные функции ограниченной вариации на [а, b], то f+g и fg - функции ограниченной вариации на [а, b].

(Утверждение, касающееся суммы f+g, верно и для вектор-нозначных функций; доказательство не меняется.)

Доказательство. Для любого разбиения сегмента [а, b] имеем

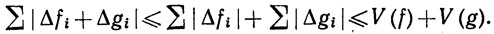
Значит, V(f+g)≤ ∑(f)+V(g), и первая часть теоремы доказана.

Теперь выберем А и В так, что 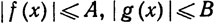на [а, b].

Если h = fg, то

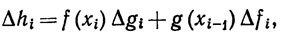
поэтому

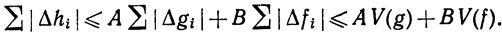
Значит, V(fg)≤AV(g)+BV(f). Тем самым доказана вторая часть.

Следствие. Если f и g монотонно возрастают на [а, b], то f-g есть функция ограниченной вариации на [а, b]. Обратное утверждение тоже верно (см. теорему 6.27).

6.25. Определение. Пусть f отображает сегмент [а, b] в пространство R^k, и пусть f - функция ограниченной вариации. Положим

(38)

Назовем v_f функцией полной вариации функции f; v_f, очевидно, монотонно возрастает на [а, b] и v_f(a) = 0.

6.26. Теорема. Пусть f - функция ограниченной вариации, отображающая сегмент [а, b] в пространство R^k.

(b) Если функция f непрерывна на [а, b], то и функция v_f тоже непрерывна на [а, b].

Доказательство. Если х = а или у = х, то равенство (39) тривиально, так как V(f; х, х) = 0. Допустим, что a<x<yу и задано число ε>0. Существует разбиение {x_i} сегмента [а, у], такое, что

(40)

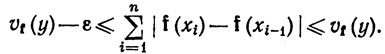
Если точка х не находится среди точек x_i, то мы добавим ее к набору {x_i} и получим таким образом новое разбиение Р, для которого неравенство (40) все еще выполняется.

Правая часть неравенства (39) оказывается верхней гранью множества всех сумм, фигурирующих в (40). Значит,

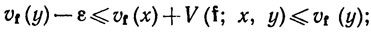
поскольку ε произвольно, равенство (39) доказано.

Теперь допустим, что функция f непрерывна, а<y≤b и

(41)

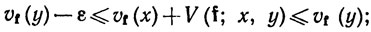
при некотором фиксированном δ>0 и при каждом х∈[а, у). (Это приведет к противоречию.) Взяв в (41) х = а, мы увидим, что существует разбиение {x_i} сегмента [а, у], такое, что

(42)

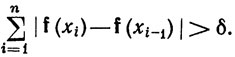
Заметим, что х_n = у, х_n-1<у. Ввиду того что f непрерывна, существует точка аи такая, что х_n-1&38804;а_i<у и величины |f(y)-f(x_n-1)| и |f(a_i)-f(x_n-1)| отличаются сколь угодно мало; в частности, (42) выполняется, если заменить у таким числом а₁.

Иными словами, мы доказали, что существует а₁<y такое что V(f; a, a_i)>δ.

Продолжим этот процесс, взяв a₁ вместо а, и т. д.; мы получим для каждого N числа

такие, что V(f; а_i-1, a_i)>δ (1≤i&38804;N).

Но отсюда в силу (39) следует, что v_f(y) ≥ Nδ при любом N, что невозможно.

Это противоречие показывает, что

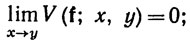
в силу (39) отсюда вытекает, что функция и, непрерывна слева на (а, b]. Тем же способом доказывается непрерывность справа на [а, b).

Замечание. Справедлива обратная теорема; формулировку можно найти в упражнении 6.

6.27. Теорема. Если f - вещественная функция ограниченной вариации на [а, b], то существуют монотонно возрастающие на [а, b] функции р и q, такие, что p(a) = q(a) = 0 и

(43)

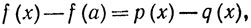
(a≤x≤b)

(44)

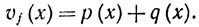
Мы будем называть р и q соответственно функциями положительной и отрицательной вариации функции f; равенство (43) показывает, что функция f представима в виде разности двух монотонных функций.

Доказательство. Определим р и q равенствами

(45)

Ясно, что p(a) = q(a) = 0 и выполняются равенства (43) и (44). Если

то (39) показывает, что

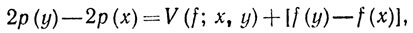
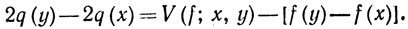
Ввиду того что |f(y)-f(x)|≤V(f; x, у), из (46) следует, что обе функции р и q - возрастающие.

Следствие 1.Если f, кроме того, непрерывна на [а, b], то тем же свойством обладают р и q.

Это вытекает из теоремы 6.26 (b) и равенств (45).

Следствие 2.Если f - функция ограниченной вариации на [а, b], то f(x+) существует при a≤x&360;b, f(х-) существует при всех a<x≤bb и множество точек разрыва функции f не более чем счетно.

Это следует непосредственно из теоремы 6.22, разложения (43) и аналогичных фактов, относящихся к монотонным функциям (теоремы 4.29 и 4.30).

Представление вещественной функции ограниченной вариации в виде разности двух монотонных функций, конечно, не единственно; в самом деле, прибавляя одну и ту же возрастающую функцию к р и q, мы получим две возрастающие функции p₁ и q₁, o такие, что f(x)-f(a) = p₁(x)-q₁(x). Однако разложение (43) обладает некоторым свойством минимальности, выделяющим его среди всех прочих разложений такого рода (см. упражнение 10).