Интегрирование векторнозначных функций

6.18. Определение. Пусть f₁, ..., f_k - вещественные функции на [а, b], и пусть f = (f₁, ..., f_k) - соответствующее отображение сегмента [а, b] в пространство R^k. Пусть функция α монотонно возрастает на [а, b]. Мы будем говорить, что f∈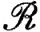(α), если f_j∈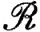(α) при j = 1, ..., k. В этом случае мы, по определению, полагаем

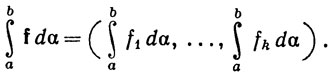
Иными словами, 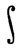f dα - это точка пространства R^k, j-я координата которой равна 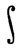f_jd.

Ясно, что утверждения (а), (с), (е) теоремы 6.10 верны и для этих векторнозначных интегралов; нужно просто применить прежние результаты к каждой координате. То же верно в отношении теорем 6.15 - 6.17. Для иллюстрации сформулируем аналог теоремы 6.16.

6.19. Теорема. Если f и F отображают сегмент [а, b] в пространство R^k, f∈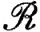 на [а, b] и F' = f, то

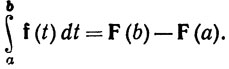
Однако аналог теоремы 6.12 (b) связан с некоторыми новыми моментами, по крайней мере в доказательстве.

6.20. Теорема. Пусть f отображает [а, b] в пространстве R^k. Если f∈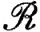(α) для какой-нибудь монотонно возрастающей на [а, b] функции α, то |f|∈(α) и

(33)

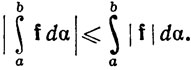
Доказательство. Если f₁, ..., f_k - компоненты отображения f, то

(34)

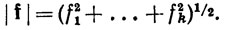
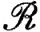По теореме 6.11 каждая из функций f²_j принадлежит множеству (α), следовательно, этому множеству принадлежит и их сумма. Поскольку x² - непрерывная функция от х, теорема 4.17 показывает, что квадратный корень - функция, непрерывная на сегменте [0, М] при каждом вещественном М. Если мы еще раз применим теорему 6.11, то увидим, что |f|∈(α).

Чтобы доказать (33), положим y = (y₁, ..., y_k), где у_j = 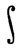f_jdα. Тогда у = 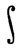fdα и

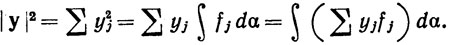
В силу неравенства Шварца,

(35)

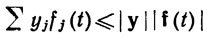
(a≤t≤b).

значит, из теоремы 6.10 (b) следует, что

(36)

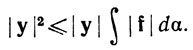
Если у = 0, то неравенство (33) тривиально. Если у≠0, то, разделив (36) на |у|, мы получим (33).