Интегрирование и дифференцирование

В этом разделе мы все еще будем заниматься вещественными функциями. Мы покажем, что интегрирование и дифференцирование являются в некотором смысле взаимно обратными операциями.

6.15. Теорема. Пусть f∈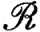 на [а, b]. Для а≤х≤b положим

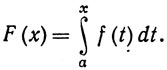
Тогда функция F непрерывна на [а, b]^*; более того, если функция f непрерывна в точке х₀∈[а, b], то функция F дифференцируема в точке х₀ и

F'(x₀) = f(x₀).

^* (Функция F не определена в точке a, ибо символу 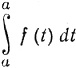не приписывалось никакого смысла (в п. 2.19 при определении сегмента как одномерной клетки сегменты вида [а, а] были исключены из рассмотрения). Для того чтобы все утверждения теоремы были верными, следует считать, что F(а) = 0.- Прим. перев.)

Доказательство. Функция f ограничена, так как f∈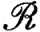. Допустим, что |f(t)|≤M, если a≤t≤b. При а≤x&360;y&38804;b имеем

по теореме 6.10 (с) и (d). Мы видим, что для данного ε>0

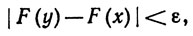
если только |y-x|<^ε/_M. Этим доказана непрерывность (и более того, равномерная непрерывность) функции F.

Допустим теперь, что функция f непрерывна в точке х₀. Для заданного ε>0 выберем δ>0 так, что

если |t-x₀|<δ и а≤t≤b. Тогда при

мы по теореме 6.10 (d) имеем

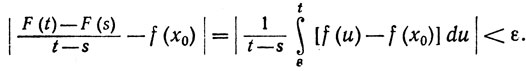
Следовательно, F'(x₀) = f(x₀).

6.16. Теорема. Если f∈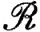 на [а, b] и существует дифференцируемая функция F на [а, b], такая, что F' = f, то

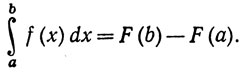
Эту теорему обычно называют основной теоремой интегрального исчисления. Ее постоянно применяют при вычислении интегралов.

Доказательство. Для данного разбиения Р сегмента [а, b] выберем t_i (i = 1, ..., n) так, что x_i-1≤t_i≤x_i и

Это возможно по теореме 5.10. Тогда

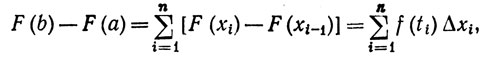
а последняя сумма стремится к 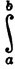f(x)dx, когда μ(P)→0, по теореме 6.14 (где α(х) = х).

6.17. Теорема. Если /?М и <х'?М на [а, ], то f∈>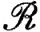(α) и

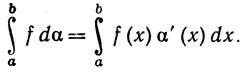
Эта теорема описывает одну из ситуаций, когда интеграл Стильтьеса сводится к интегралу Римана.

Доказательство. Заметим сначала, что по теореме 6.12 fα'∈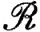. Пусть ε>0. Выберем М так, что |f|≤M. Поскольку f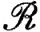α'∈ и α'∈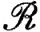, из теоремы 6.14 (b) следует, что существуют δ₁>0 и δ₂>0, такие, что

(30)

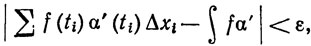
если μ(P)<δ₁ и x_i-1≤t_i̤x_i и

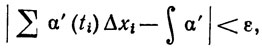
если μ(P)<δ₂ и x_i-1≤t_i̤x_i.

Если s_i - другая точка, такая, что x_i-1≤s_i̤x_i, то мы имеем

(31)

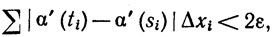
когда μ(P)<δ₂ и x_i-1≤t_i̤x_i, x_i-1≤s_i̤x_i.

Выберем теперь Р так, что μ(P)<δ = min(δ₁, δ₁,), и пусть t_i∈[x_i-1, x_i]. По теореме 5.10 существуют точки s_i∈[x_i-1, x_i], такие, что Δα_i = α'(s_i)Δx_i. Тогда

(32)

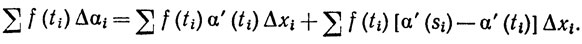
Согласно (30) и (31), левая часть равенства (32) отличается от 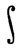fα' меньше, чем на (2M + 1)ε. Это означает, что

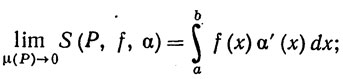
принимая во внимание теорему 6.14 (a), мы приходим к требуемому заключению.