Интеграл как предел сумм

До сих пор мы определяли интеграл при помощи сумм U(P, f, α), L(P, f, α). Однако числа M_i, m_i, появляющиеся в этих суммах, не обязательно служат значениями функции f (они действительно оказываются значениями функции f, если f непрерывна). Сейчас мы покажем, что интеграл ∫ f da можно рассматривать как предел последовательности сумм, в которых M_i и m_i заменены значениями функции f. Как и выше, а монотонно возрастает, а f ограничена и вещественна на [а, b].

6.13. Определение. Пусть Р - какое-нибудь разбиение сегмента [а, b]. Выберем точки t₁, ..., t_n так, что x_i-1≤t_i≤x_i (i = 1, ..., n), и рассмотрим сумму

(22)

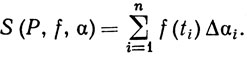
Положим, по определению,

(23)

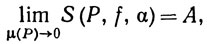
если для любого ε>0 существует δ>0, такое, что при μ(P)<δ имеем

(24)

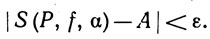
Отметим, что обозначение S (Р, f, α) на самом деле неполно, так как сумма (22) зависит еще и от выбора точек t_i удовлетворяющих условию x_i-1≤t_i≤x_i. Но это не может привести ни к какому недоразумению, если мы будем помнить, что соотношение (23) означает справедливость неравенства (24) при всяком Р и всяком допустимом выборе точек t_i, если только μ(P) <δ.

6.14. Теорема. (а) Если lim S(P, f, α) при μ(P)→0 существует, то f∈(α) и

(25)

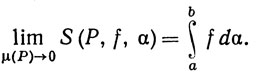
(b) Если (i) f непрерывна или если (ii) f&38712;(α) и α непрерывна на [а, b], то выполняется соотношение (25).

Упражнение 4 покажет, что требование непрерывности в утверждении (b) не может быть опущено.

Доказательство. Допустим сначала, что предел в левой части равенства (25) существует и равен А. Пусть задано число ε>0.

Существует δ>0, такое, что при μ(P)<δ имеем

(26)

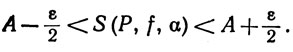
Выберем такое Р. Если мы заставим точки t_i пробегать сегменты [x_i-1,x_i] и возьмем верхнюю и нижнюю грани чисел S (Р, f, α), полученных таким образом, то, принимая во внимание (26), мы придем к неравенству

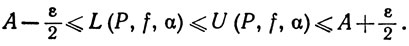
По теореме 6.6 f∈(α) это завершает доказательство утверждения (а), так как

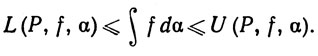
Часть (i) утверждения (b) содержится в теореме 6.8. Чтобы доказать часть (ii), допустим, что f∈(α), функция α непрерывна и ε>0. Существует разбиение Р^*, такое, что

(27)

Положим

Поскольку функция а равномерно непрерывна на [a, b], существует δ₁&362;0, обладающее следующим свойством: если Р - любое разбиение сегмента [а, b], такое, что μ(P)<δ₁, то Δα_i<ε/4Mn при всех i, где n - число сегментов разбиения Р^*. Пусть Р - любое разбиение, такое, что μ(P)<δ₁. Рассмотрим сумму U(P, f, α). Вклад в эту сумму тех сегментов разбиения Р, внутри которых содержится точка разбиения Р^*, не превышает величины

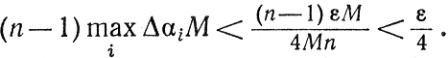
В соединении с (27) это дает

(28)

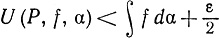
при всех Р, для которых μ(P)<δ₁.

Точно таким же способом мы можем показать, что существует число δ₂>0, такое, что

(29)

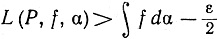
при всех Р, для которых μ(P)<δ₂.

Выбирая δ = min (δ₁, δ₂), мы видим, что неравенства (28) и (29) выполняются при каждом Р, таком, что μ(Р)<δ. Поскольку, очевидно,

из (28) и (29) следует, что

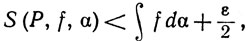
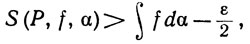
а из этих двух последних неравенств видно, что

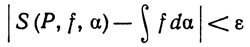
при всех Р, таких, что μ(P)<δ. Доказательство закончено.