Определение и существование интеграла

6.1. Определение. Пусть [а, b] - заданный сегмент. Разбиением Р сегмента [а, b] мы называем конечное множество точек х₀, х₁, ... ,х_n, где

Мы будем писать

Пусть теперь f - ограниченная вещественная функция, определенная на [а, b]. Каждому разбиению Р сегмента [а, b] соответствуют числа

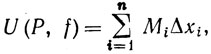
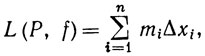
и, наконец,

(1)

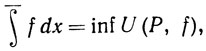
(2)

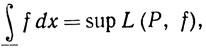
где верхняя и нижняя грани берутся по всем разбиениям Р сегмента [а, b]. Левые части равенств (1) и (2) называются соответственно верхним и нижним интегралами Римана функции f по сегменту [а, b].

Если верхний интеграл равен нижнему, то мы будем говорить, что функция f интегрируема по Риману на сегменте [а, b] и писать f∈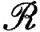 (иными словами, 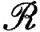обозначает множество всех функций, интегрируемых по Риману), а общее значение величин (1) и (2) будем обозначать

(3)

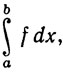
или

(4)

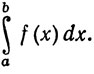
Это - интеграл Римана от функции f по сегменту [а, b]. Поскольку f ограничена, существуют два числа m и М, такие, что

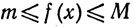
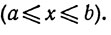
Значит, при любом разбиении Р

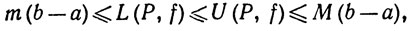
так что числа L(P, f) и U(P, f) образуют ограниченное множество. Это показывает, что верхний и нижний интегралы определены для любой ограниченной функции f. Вопрос об их совпадении и, значит, вопрос об интегрируемости функции f оказывается более тонким. Вместо того чтобы исследовать его отдельно для интеграла Римана, мы сейчас рассмотрим более общую ситуацию.

6.2. Определение. Пусть α - монотонно возрастающая функция на [а, b] (поскольку α(а) и α(b) конечны, функция а ограничена на [а, b]). Если Р - какое-нибудь разбиение сегмента [а, b], то положим

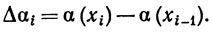
Ясно, что Δα_i≥0. Для любой вещественной функции f, ограниченной на [а, b], положим

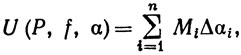
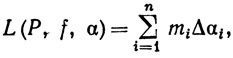
где M_i и m_i имеют тот же смысл, что и в определении 6.1. Положим, по определению,

(5)

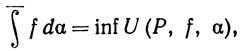
(6)

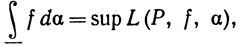
где верхняя и нижняя грани берутся снова по всем разбиениям. Если левые части равенств (5) и (6) равны между собой, то их общее значение обозначается через

(7)

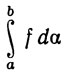
или иногда через

(8)

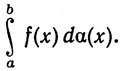
Это - интеграл Римана-Стильтьеса (или просто интеграл Стильтьеса) от функции f относительно функции а по сегменту [а, b].

Если интеграл (7) существует, т. е. если (5) и (6) равны между собой, то мы будем говорить, что f интегрируема относительно а в смысле Римана, и писать f∈(α).

Полагая α(х) = х, мы приходим к выводу, что интеграл Римана - это частный случай интеграла Римана-Стильтьеса. Подчеркнем, однако, что в общем случае функция а не обязана быть даже непрерывной.

Несколько слов по поводу обозначений. Мы предпочитаем обозначение (7) обозначению (8), так как фигурирующая в (8) буква х ничего не добавляет к содержанию записи (7). Совершенно несущественно, какую букву мы употребляем для обозначения так называемой "переменной интегрирования". Так, например, (8) - это то же самое, что

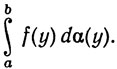
Интеграл зависит от f, α, а и b, но не от переменной интегрирования, которую вполне можно опустить.

Роль переменной интегрирования совершенно аналогична роли индекса суммирования: два символа

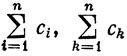
означают одно и то же, а именно сумму c₁+с₂+...+c_n.

Разумеется, не произойдет ничего страшного, если переменная интегрирования будет написана, а в некоторых случаях даже удобно ее писать.

Теперь мы исследуем вопрос о существовании интеграла (7).

Не повторяя этого каждый раз, мы будем считать функцию f вещественной и ограниченной, а функцию α - монотонно возрастающей на [а, b], и если исключена возможность недоразумений, мы будем писать вместо

6.3. Определение. Мы будем говорить, что разбиение Р^* является измельчением разбиения Р, если Р^*⊃P (т. е. если каждая точка разбиения Р служит также точкой разбиения Р^*). В случае, когда заданы два разбиения P₁ и Р₂, мы будем говорить, что Р^* есть их общее измельчение, если P^* = P₁∪P₂.

6.4. Теорема. Если Р^* - измельчение разбиения Р, то

(9)

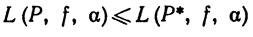
и

(10)

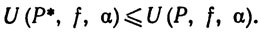
Доказательство. Чтобы доказать неравенство (9), допустим сначала, что Р^* содержит ровно на одну точку больше, чем Р. Обозначим эту новую точку через х^* и допустим, что x_i-1≤x^*≤x_i, где x_i-1 и x_i - две последовательные точки разбиения Р. Положим

Ясно, что ω₁≥m_i и ω₁≥m_i, где, как и прежде,

Значит,

Если Р^* содержит на k точек больше, чем Р, то мы повторим только что проведенное рассуждение k раз и получим (9). Доказательство неравенства (10) аналогично.

6.5. Теорема.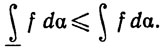

Доказательство. Пусть Р^* - общее измельчение двух разбиений P₁ и Р₂. По теореме 6.4

Значит,

(11)

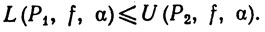
Считая Р₂ фиксированным и вычисляя верхнюю грань по всем Р₁, получаем из (I1)

(12)

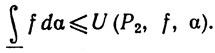
Вычисляя нижнюю грань по всем Р₂ в (12), получаем утверждение теоремы.

6.6. Теорема. f∈(α) на [а, b] тогда и только тогда, когда для любого ε>0 существует разбиение Р, такое, что

(13)

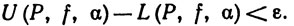
Доказательство. При любом Р имеем

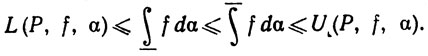
Поэтому из (13) следует, что

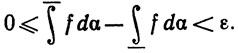
Значит, если при любом ε>0 неравенству (13) удовлетворяет некоторое разбиение Р, то

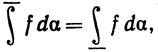
т.е. f∈(α)

Допустим теперь, что f∈(α) и задано число ε?№62ж0. Тогда существуют разбиения Р₁ и Р₂, такие, что

(14)

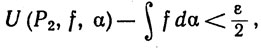
(15)

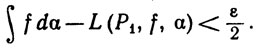
Выберем в качестве Р общее измельчение разбиений P₁ и Р₂. Тогда, как показывает теорема 6.4 вместе с неравенствами (14) и (15),

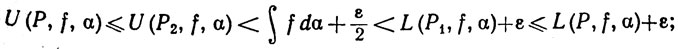
для такого разбиения Р выполняется неравенство (13).

Теорема 6.6 позволит нам доказать интегрируемость двух важных классов функций. Но сначала введем еще одно определение.

6.7. Определение. Для любого разбиения Р положим

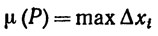
(1≤i≤n)

и назовем μ(Р) диаметром разбиения Р.

6.8. Теорема. Если функция f непрерывна на [а, и], то f∈(α) на [а, и]. Более того, каждому ε?№62ж0 отвечает такое δ>0, что

(16)

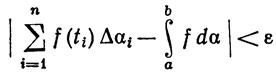
для любого разбиения Р = {х₀, х₁, ..., х_n} сегмента [а, b], удовлетворяющего условию μ(P)<δ, и при любом выборе точек t₁ в сегменте [x_i-1, x_i].

Доказательство. Пусть задано число ε>0, и пусть η>0 таково, что

Поскольку f равномерно непрерывна на [a, b] (теорема 4.19), существует такое δ>0, что

(17)

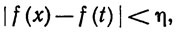
если |х -t|<δ и х∈[а, b], t∈[a, b].

Выберем Р так, что μ(P)<δ. Тогда из неравенства (17) следует, что

Значит,

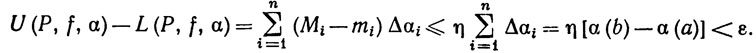
Итак, по теореме 6.6, f∈(α).

Неравенство (16) также доказано, так как оба числа 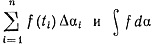лежат между U (Р, f, α) и L(P, f, α).

6.9. Теорема. Если f монотонна на [а, b], а α непрерывна на [а, b], то f∈(α) (мы по-прежнему предполагаем, разумеется, что α монотонна).

Доказательство. Пусть задано ε>0. Для любого положительного n выберем разбиение Р так, что

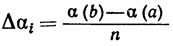
(i = 1, .., n).

Это возможно, так как функция α непрерывна (теорема 4.23). Предположим теперь, что f монотонно возрастает (в другом случае доказательство аналогично). Тогда

так что

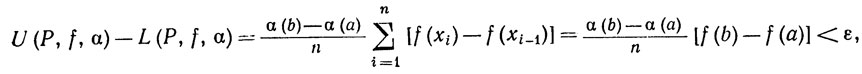
если n достаточно велико. По теореме 6.6 f∈(α).

Теперь мы докажем некоторые элементарные свойства интеграла Стильтьеса.

6.10. Теорема, (а) Если f₁∈(α) и f₂∈(α) на [а, b], то f₁+f₂∈(α), cf∈(α), какова бы ни была константа с, и

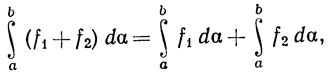
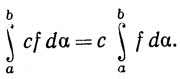
(b) Если f₁(x)≤f₂(x) на [а,b], то

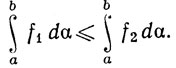
(c) Если f∈(α) на [а, b] и если а<с<b, то f∈(α) на [а, с] и на [с, b] и

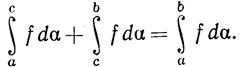
(d) Если f∈(α) на [a, b] и если |f(x)|≤M на [a, b], тo

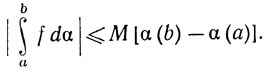
(e) Если f∈(α₁) и f∈(α₂), то f∈(α₁+α₂) и

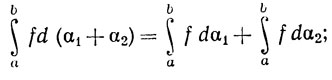
если f∈(α) и с - положительное число, то f∈(cα) и

Доказательство. Если f = f₁ + f₂, a Р - какое-нибудь разбиение сегмента [а, b], то

(18)

Если f₁∈(α) и f₂∈(α), то любому числу ε>0 отвечают такие разбиения P_j (j = 1, 2), что

Это неравенство сохранится, если Р₁ и Р₂ заменить их общим измельчением Р. Тогда из (18) следует, что

а это значит, что f∈(α).

Для этого же разбиения Р имеем

таким образом, из (18) следует, что

Ввиду произвольности ε мы приходим к неравенству

(19)

Если заменить f₁ и f₂ в (19) функциями -f₁ и -f₂, то неравенство изменится на обратное (ибо, как легко проверить, ∫(-f)dα = -∫fdα); тем самым доказано требуемое равенство.

Доказательства остальных утверждений теоремы 6.10 совершенно аналогичны. В части (с) все дело в том, что, переходя к измельчениям при приближении интеграла ∫fdα, мы можем ограничиться лишь разбиениями, содержащими точку с.

6.11. Теорема. Пусть f∈(α) на [a, b], m≤f≤M, φ непрерывна на [m, М] и h(x) = φ(f(x)) на [a, b]. Тогда h∈(α) на [a, b].

Доказательство. Выберем ε<0. Ввиду того что φ равномерно непрерывна на [m, М], существует δ>0, такое, что δ<ε 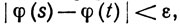и если 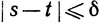и s, t∈ [m, M].

Поскольку f∈(α), существует разбиение Р = {х₀, х₁, ..., х_n} сегмента [а, b], такое, что

(20)

Пусть M_i и m_i имеют тот же смысл, что и в определении 6.1, и пусть М^*_i, m^*_i - аналогичные величины для функции h. Разобьем числа 1, ..., n на два класса: i∈A, если М_i-m_i<δ; i∈B, если M_i-m_i≥δ.

Для i∈A, в силу выбора δ, оказывается, что М_i-m_i≤ε.

Для i∈B имеем М_i-m_i≤2K, где K = sup|φ(t)|, m≤t≤M.

Согласно (20), имеем

(21)

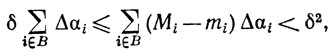
так что 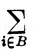Δα_j<δ. Следовательно,

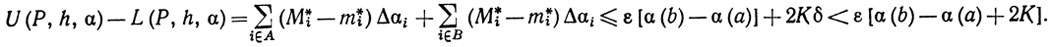
Теперь из теоремы 6.6 следует, что h∈(α), так как число е произвольно.

Замечание. Эта теорема подсказывает такой вопрос: какие же функции интегрируемы по Риману? Ответ дается в теореме 10.33(b).

6.12. Теорема. Если f∈(α) и g∈(α) на [а, b], то

(b)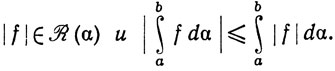

Доказательство. Полагая φ(t) = t² и применяя к φ теорему 6.11, мы видим, что f²∈(α), если f∈(α). Тождество

завершает доказательство утверждения (а).

Полагая φ(t) = |t| и применяя теорему 6.11, мы точно так же убеждаемся в том, что |f|∈(α). Выберем с = ± 1 так, что

Тогда 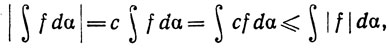так как cf≤|f|.