Упражнения

1. Пусть 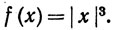Вычислить f'(х), f'(x) при всех вещественных х и показать, что f⁽³⁾(0) не существует.

2. Пусть f определена при всех вещественных х, и пусть

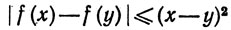
при всех вещественных х и у. Доказать, что f постоянна.

3. Пусть f определена в окрестности точки x, и пусть существует f"(x). Показать, что

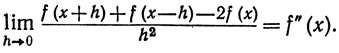
Показать на примере, что этот предел может существовать и тогда, когда f"(х) не существует.

4. Пусть

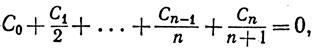
где С₀, ..., С_n - вещественные постоянные. Доказать, что уравнение

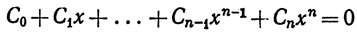
имеет хотя бы один вещественный корень между 0 и 1.

5. Пусть f определена и дифференцируема при каждом x>0 и f'(х)→0 при x→+ ∞. Положим g(x) = f(x+1)-f(x). Доказать, что g(x)→0 при х→+ ∞ .

6. Пусть

(a) f непрерывна при x≥0,

(b) f (х) существует при всех x>0,

(c) f(0) = 0,

(d) f монотонно возрастает.

Положим

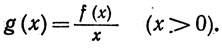
Доказать, что g монотонно возрастает.

7. Пусть f'(x), g'(х) существуют, g'(х)≠ и f(х) = g(х) = 0. Доказать, что

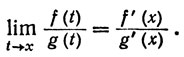
(это верно и для комплексных функций.)

8. Пусть f'(x)>0 при всех х∈(а, b). Доказать, что f строго возрастает в интервале (а, b). Пусть g - функция, обратная к f. Доказать, что g дифференцируема и что

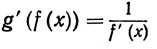
(a<x<b).

9. Пусть f дифференцируема в интервале (а, b), a<x<b, x<α_n<β_n при n = 1, 2, 3, ... и α_n→х, β_n→х. Показать, что отношения

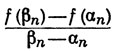
не обязательно сходятся к f'(х) при n→∞, но что они действительно сходятся к f'(x), если мы дополнительно потребуем, чтобы последовательность {(β_n-х)/(β_n-α_n)} была ограниченной.

10. Пусть f и g - комплексные дифференцируемые функции на (0, 1), f(x)→0, g(x)→0, f'(x)→A, g'(x)→B при x→0, где А и B - комплексные числа, ≠0. Доказать, что

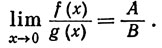
(Ср. с примером 5.18.)

Указание:

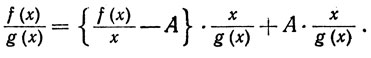
Применить теорему 5.13 к вещественной и мнимой частям дробей ^f(x)/_x и ^g(x)/_x.

11. Сформулировать и доказать неравенство, которое следует из теоремы Тейлора и остается верным для векторнозначных функций.

12. Пусть Е - замкнутое подмножество прямой R¹. В упражнении 13 гл. 4 было показано, что существует вещественная непрерывная функция в R¹ нуль-множество которой совпадает с Е. Можно ли для каждого замкнутого множества Е найти такую дифференцируемую на R¹ функцию f, для которой Е служит нуль-множеством? Существует ли n раз дифференцируемая функция с таким свойством? Функция, которая имеет производные всех порядков на R¹?

13. Пусть g - вещественная функция на R¹, имеющая ограниченную производную (скажем, 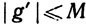). Зафиксируем ε>0 и положим f(x) = х+εg(x). Доказать, что f взаимно однозначна, если число ε достаточно мало. (Можно определить множество допустимых ε, зависящее лишь от М.)

14. Пусть f - дважды дифференцируемая вещественная функция на (0, ∞), и пусть М₀, М₁, М₂ - верхние границы соответственно функций |f|, |f'|, |f"| на (0, ∞). Доказать, что М₁²≤4М₀М₂.

Указание. Из теоремы Тейлора следует, что

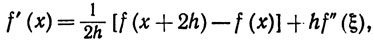
так что |f'|≤hM₂ + M₀/h при любом h>0.

Можно ли этот результат распространить на векторнозначные функции?

15. Пусть f дважды дифференцируема на (0, ∞), f" ограничена на (0, ∞) и f(x)→0 при х→∞. Доказать, что f'(x)→0 при х→∞.

Указание. Применить упражнение 14 на (а, ∞). Показать, что это утверждение становится неверным, если опустить предположение о f".

16. Пусть f дифференцируема на [а, b], f(а) = 0 и существует вещественное число А, такое, что 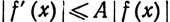на [а, b]. Доказать, что f(x) = 0 при всех х∈[а, b].

Указание. Зафиксируем х₀∈[а, b], и пусть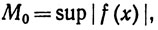

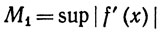
на сегменте [а, x₀]. Для любого х∈[а, х₀]

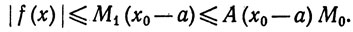
Значит, М₀ = 0, если А(х₀ - а)<1, т. е. f = 0 на [а, x₀]. Продолжить это рассуждение.

17. Пусть φ - вещественная функция, определенная в прямоугольнике R на плоскости, заданном неравенствами а≤x≤b, α≤y≤β. Решением задачи с начальными условиями

называется дифференцируемая на [a, b] функция f, такая, что f(a) = c и

Доказать, что эта задача имеет не более одного решения, если существует число А, такое, что

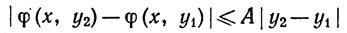
для любых (х, y₁)∈R, (x, y₂)∈R.

Указание. Применить упражнение 16 к разности двух решений. Заметим, что эта теорема единственности неприменима к задаче с начальными условиями

которая имеет два решения: f(x) = 0 и f(x) = ^x2/₄. Имеются ли другие решения?

18. Сформулировать и доказать аналогичную теорему единственности для системы дифференциальных уравнений вида

Заметим, что эту систему можно записать в виде

где у = (y₁, .. .,у_k) пробегает k-мерную клетку, φ - отображение некоторой (k+1)-мерной клетки в евклидово пространство R^k, причем компонентами φ служат функции φ₁, ..., φ_k, а с - вектор (c₁, ..., c_k). Воспользоваться упражнением 16 для векторнозначных функций.

19. Рассмотреть частный случай упражнения 18, перейдя к системе

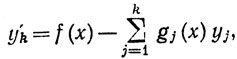
где f, g₁, ...,g_k - непрерывные вещественные функции на [а, b], и получить теорему единственности для решений уравнения

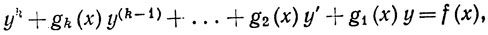
удовлетворяющих начальным условиям

20. Пусть f непрерывна на [а, b] и ε>0. Доказать, что существует число δ>0, такое, что

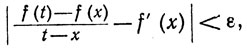
если 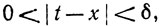a≤x≤b, a≤t≤b. (Это значит, иными словами, что f равномерно дифференцируема на [а, b], если f'непрерывна на [а, b].) Верно ли это для векторнозначных функций?