Дифференцирование векторнозначных функций

5.16. Замечания. Определение 5.1 без всяких изменений применимо к комплексным функциям f, определенным на [а, b]. При этом теоремы 5.2 и 5.3 остаются верными, так же как и их доказательства. Если f₁ и f₂ - вещественная и мнимая части функции f, т. е. если f(t) = f₁(t) + if₂(t) при а<6, где МО и МО вещественны, то, очевидно, (29) >

причем f дифференцируема в точке х тогда и только тогда, когда обе функции f₁ и f₂ дифференцируемы в этой точке.

Переходя к общим векторнозначным функциям, т. е. к функциям f, отображающим [а, b] в некоторое пространство R^k, мы все еще можем применить определение 5.1 для построения f'(х). Теперь φ(t) в формуле (1) при каждом t является точкой пространства R^k, а предел в (2) вычисляется в смысле сходимости по норме этого пространства. Иными словами, f'(х) - это та точка пространства R^k (если она существует), для которой

(30)

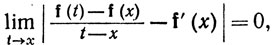
и f' - снова функция со значениями в R^k.

Если f₁, ...,f_k - компоненты функции f, определенные в теореме 4.10, то

(31)

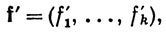
и функция f дифференцируема в точке х тогда и только тогда, когда каждая из функций f₁, ..., f_k дифференцируема в точке х.

Теорема 5.2 остается верной и в этом случае; то же относится и к теореме 5.3 (а) и (Ь), если fg заменить скалярным произведением fg (см. определение 4.3).

Однако, когда мы обращаемся к теореме о среднем значении и к правилу Лопиталя, положение меняется. Следующие два примера показывают, что оба эти результата неверны уже для комплекснозначных функций.

5.17. Пример. Положим для вещественного х

(32)

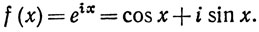
(Последнее выражение можно рассматривать как определение комплексной показательной функции е^ix. Эти функции будут подробно рассмотрены в гл. 8.) Тогда

(33)

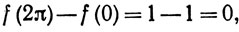
но

(34)

так что |f'(х)| = 1 при всех вещественных х.

Таким образом, в этом случае теорема 5.10 уже неверна.

5.18. Пример. На интервале (0,1) зададим функции f, g, полагая f(x) = x и

(35)

Поскольку |e^it| = 1 при всех вещественных t, мы видим, что

(36)

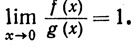
Далее,

(37)

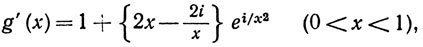
так что

(38)

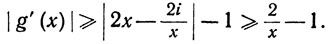
Значит,

(39)

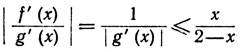
и поэтому

(40)

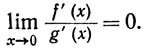
Сопоставляя (40) с (36), мы видим, что правило Лопиталя в этом случае не действует. Отметим еще, что g'(x)≠0 на интервале (0,1), в силу (38).

Однако имеется все-таки одно следствие теоремы о среднем значении, которое в приложениях почти так же полезно, как теорема 5.10, и которое остается верным для векторнозначных функций: из теоремы 5.10 следует, что

(41)

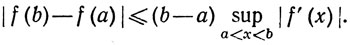
Прежде чем установить векторный аналог неравенства (41), мы приведем теорему, показывающую, что при вычислении производной можно пользоваться отношениями, отличными от тех, которые фигурировали в определении 5.1. Не ограничиваясь случаем k = 1, рассмотрим общий случай.

5.19. Теорема. Пусть a<x<b, функция f отображает [а, b] в пространство R^k и пусть f дифференцируема в точке х. Пусть а<α_n<х<β_n<b при n = 1, 2, 3,..., и пусть α_n→x, β_n→x. Тогда

(42)

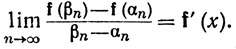
Доказательство. Положим λ_n = (β_n-х)/(β_n-α_n). Тогда 0<λ_n<1, и вектор

(43)

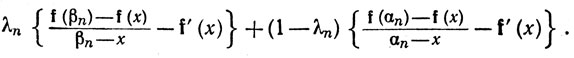
при каждом n равен вектору

(44)

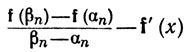
По определению 5.1, оба выражения в скобках стремятся к 0, и так как последовательности {λ_n} и {1-λ_n} ограничены, то вектор (44), а с ним и (43) стремится к нулю при n→∞. Равенство (42) доказано.

5.20. Теорема. Пусть f - непрерывное отображение сегмента [а, b] в пространство R^k, дифференцируемое в интервале (а, b). Тогда существует точка х∈(а, b), такая, что

(45)

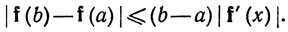
Доказательство. Положим 3L = b - a, M = |f(b) - f(a)| и

(46)

Поскольку

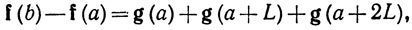
мы видим, что

(47)

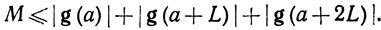
Если бы оказалось, что |g(s)|<^M/₃ при всех s∈(a, a+2L), то из непрерывности отображения g следовало бы, что |g(a)|≤^М/₃, |g(a+2L)|≤^M/₃, и, значит, правая часть неравенства (47) была бы меньше М.

Следовательно, |g(s₁)|≥^М/₃ при некотором s₁∈(а, а+2L). Полагая t₁ = s₁+L, мы находим, что a<s₁<t₁<b, t₁ - s₁ = (b - a)/3 и

(48)

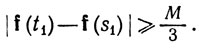
Повторим это построение, взяв [s₁, t₁] вместо [a, b]. Продолжая таким образом, мы найдем две последовательности {s_n}, {t_n}, такие, что

каждый сегмент I_n = [s_n, t_n] содержится внутри сегмента I_n-1 и

(50)

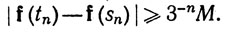
Разделив (50) на (49), мы получим

(51)

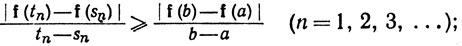
из теоремы 5.19 мы заключаем, что (45) выполнено для точки х, принадлежащей всем сегментам I_n^*.

^* (Вот другое, значительно более короткое доказательство теоремы 5.20. Рассмотрим числовую функцию φ, заданную на [а, b] равенством: φ(t) = (f(b)) - f(a))*f(t). К этой функции можно применить теорему о среднем значении: φ(b)-φ(а) = φ'(х)*(b-а), где х - некоторая точка интервала (а, b). Теперь остается заметить, что φ(b)-φ(a) = |f(b)-f(а)|², а φ'(x) = (f(b)-f(a))*f'(x) (см. по этому поводу предпоследний абзац п. 5.16), и поэтому |f(b)-f(a)|² = (f(b)-f(a))*f'(x)*(b-а). Применяя к правой части этого равенства неравенство Шварца, получим

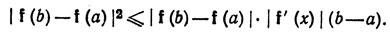
Теорема доказана.- Прим. перев.)