Теорема Тейлора

5.15. Теорема. Допустим, что f - вещественная функция на [а, b], n - положительное целое число, f^(n-1) непрерывна на [а, b], f⁽ⁿ⁾(t) существует в любой точке t∈(a, b). Пусть а, р - различные точки сегмента [а, b]. Положим

(23)

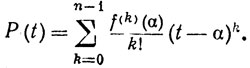
Тогда существует точка х, лежащая между α и β, такая, что

(24)

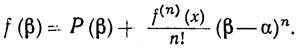
При n = 1 это утверждение превращается в теорему о среднем значении. В общем случае теорема показывает, что функцию f можно приблизить многочленом степени n-1; равенство (24) позволяет оценить погрешность, если известна верхняя граница величины |fⁿ(x)|.

Доказательство. Пусть М - число, определяемое равенством

(25)

и пусть

(26)

Мы должны показать, что n!M = fⁿ(x) при некотором х, лежащем между α и β. Согласно (23) и (26),

(27)

Значит, доказательство будет закончено, если мы проверим, что g⁽ⁿ⁾(х) = 0 при некотором х, лежащем между α и β.

Поскольку P^(k)(a) = f^(k)(a) при k = 0,...,n-1, мы имеем

(28)

Число М было выбрано так, что g(β) = 0; поэтому, согласно теореме о среднем, g'(x₁) = 0 при некотором хи лежащем между α и β. Так как g'(α) = 0, то подобным же образом мы заключаем, что g"(х₂) = 0. при некотором х₂, лежащем между α и x₁. После n шагов мы придем к выводу, что g⁽ⁿ⁾(x_n) = 0 при некотором х_n, лежащем между α и х_n-1, т. е. между α и β.