Правило Лопиталя

Следующая теорема часто бывает полезной при вычислении пределов.

5.13. Теорема. Пусть f и g вещественны и непрерывны в интервале (а, b) и g'(х)≠0 при всех х∈(а, Ь), где -∞≤a<b≤+∞. Пусть

(13)

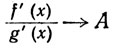
при x→a.

Если

(14)

f(x)→0 и g(x)→0 при x→a,

или если

(15)

g(x)→+∞ при x→a,

то

(16)

при х→а.

Аналогичное утверждение, конечно, верно и тогда, когда х→b или когда в (15) g(x)→-∞. Заметим, что сейчас мы используем понятие предела в расширенном смысле в соответствии с определением 4.33.

Доказательство. Сначала предположим, что -∞≤A<+∞. Выберем вещественное число q, такое, что A<q, а затем выберем r так, чтобы выполнялось неравенство А<r<q. Согласно (13), существует точка с∈(а, b), такая, что при а<x<c имеем

(17)

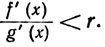
Если а<x<y<c, то, как показывает теорема 5.9, существует точка t∈(х, у), такая, что

(18)

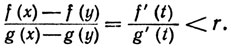
Допустим, что выполнено условие (14). Устремляя в (18) х к а, мы видим, что

(19)

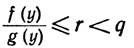
(a<y<c).

Теперь допустим, что выполнено условие (15). Считая у в формуле (18) фиксированным, мы можем выбрать такую точку c₁∈(a, у), что g(x)>g(у) и g(x)>0, если a<x<c₁. Умножая (18) на [g(x) - g(y)]/g(x), мы получим

(20)

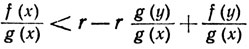
(a<x<c₁).

Если в (20) устремить х к а, то, как показывает (15), можно найти точку с₂∈(a, c₁), такую, что

(21)

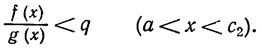
Итак, неравенства (19) и (21) показывают, что для любого q, подчиненного единственному условию A<q, найдется точка с₂∈(а, b), такая, что f(x)/g(х)<q, если a<x<c₂.

Точно таким же способом в том случае, когда - ∞<А≤+ ∞, а р выбрано так, что p<А, мы найдем точку с₃∈(а, b), такую, что

(22)

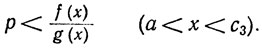
Из этих двух утверждений следует соотношение (16).