Непрерывность производных

Мы уже видели [пример 5.6 (b)], что функция f может иметь производную f', которая существует во всех точках, но разрывна в некоторых точках. Однако не каждая функция может быть производной. В частности, производные, которые существуют в каждой точке некоторого сегмента, так же как и функции, непрерывные на сегменте, обладают следующим важным свойством: они принимают промежуточные значения (ср. с теоремой 4.23). Точная формулировка такова.

5.12. Теорема. Пусть f - вещественная функция, дифференцируемая на [а, b], и пусть f'(а)<λ<f'(b). Тогда существует точка х∈(а, b), такая, что f(х) = λ.

Подобный результат верен, конечно, и тогда, когда f'(a)>f'(b).

Доказательство. Положим с = ¹/₂(а + b). Если a≤t#8804;c, то пусть α(t) = a, β(t) = 2t-а. Если с≤t≤b, то пусть α(t) = 2t - b, β(t) = b. Тогда а≤α(t)<β(t)≤b в интервале (а, b). Положим

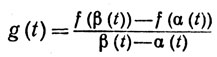
Тогда g непрерывна на (a, b), g(t)→f'(а) при t→a, g(t)→f'(b) при t→b и поэтому из теоремы 4.23^* следует, что g(t₀) = λ при некотором t₀∈(a, b). Зафиксируем t₀. По теореме 5.10 существует точка х, такая, что α(t₀)<х<β(t₀) и f'(х) = g(t₀). Значит, f'(x) = λ.

^* (В теореме 4.23 речь идет о функции, непрерывной на сегменте [а, b]. Здесь имеется в виду, что функцию g можно доопределить в точках а и b, полагая g(a) - f'(a), g(b) = f'(b), так что g станет непрерывной и в точках а, b по теореме 4.6.- Прим. перев.)

Следствие. Если f дифференцируема на [а, b], то f' не имеет простых разрывов на [а, b].

Однако f' вполне может иметь разрывы второго рода.