Теоремы о среднем значении

5.7. Определение. Пусть f - вещественная функция, определенная на метрическом пространстве X. Будем говорить, что f имеет локальный максимум в точке р∈Х, если существует δ>0, такое, что f(q)≤f(p) при всех q∈X, таких, что d(p,q)<δ.

Локальные минимумы определяются сходным образом.

Наша следующая теорема лежит в основе многих применений дифференцирования.

5.8. Теорема.Пусть функция f определена на сегменте [а, b]; если f имеет локальный максимум в точке х∈(а, b) и если существует f'(х), то f'(x) = 0.

Аналогичное утверждение, относящееся к локальному минимуму, конечно, тоже верно.

Доказательство. Выберем δ в соответствии с определением 5.7, так что

Если х-δ<t<x, то

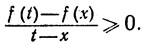
Устремляя t к х, мы видим, что f'(x)≥0.

Если x<t<x+δ, то

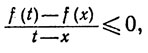
откуда следует, что f'(х)≤0. Значит, f'(х) = 0.

5.9. Теорема. Если f и g - непрерывные вещественные функции на сегменте [а, b], дифференцируемые на интервале (а, b), то существует точка х∈(а, b), в которой

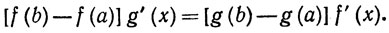
Заметим, что здесь не требуется дифференцируемость в точках а и b.

Доказательство. Положим

Функция h непрерывна на [а, b], дифференцируема на (а, b) и

(12)

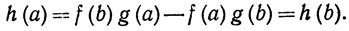
Для доказательства теоремы мы должны проверить, что h'(x) = 0 при некотором х∈(а, b).

Если h постоянна, то h'(x) = 0 при любом х∈(а, b). Если h(t)>h(a) при некотором t∈(a, b), то пусть х - та точка сегмента [а, b], в которой h достигает своего максимума (теорема 4.16). В силу (12), х∈(а, b), и теорема 5.8 показывает, что h'(х) = 0. Если h(t)<h(а) при некотором t∈(a, b), то можно применить такое же рассуждение, выбрав в качестве х ту точку сегмента [а, b], в которой h достигает своего минимума.

Эту теорему часто называют обобщенной теоремой о среднем значении; следующий ее частный случай называют теоремой о среднем значении.

5.10. Теорема. Если f - вещественная непрерывная функция на [а, b], дифференцируемая на (а, b), то существует точка х∈(а, b), в которой

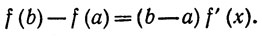
Доказательство. Положим g(х) = х в теореме 5.9.

5.11. Теорема. Пусть функция f дифференцируема в интервале (а, b).

(c) Если f'(х)≤ при всех х∈(а, b), то f монотонно убывает.

Доказательство. То, что все эти заключения справедливы, можно усмотреть из равенства

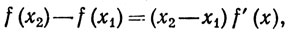
верного для любой пары чисел x₁, x₂, лежащих в (а, b) при некотором х, расположенном между х₁ и х₂.